Analysis of Tesla Stock Price in the most recnet 6 months#
Author: [Chenxi Yang]
Course Project, UC Irvine, Math 10, S24
I would like to post my notebook on the course’s website. [Yes]
The dataset I am analyzing is the 6-month data of Tesla stocks downloaded from NASDAQ website. I will be analyzing the dataset using relevant knowledge learned from Math 10.
1 Importing and Cleaning Data
In this step, I just imported some tools and imported the dataset to the notebook so that I can access it. I checked the basic information of the data, to make sure there is nothing wroing with it. It is important to mention, that since the data of Volume is too big, it is necessary to make sure the format matches that of the notebook.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import classification_report, confusion_matrix
data = pd.read_csv('tesla_stock.csv')
print(data)
pd.options.display.float_format = '{:.2f}'.format
Date Close/Last Volume Open High Low
0 6/12/2024 177.29 90389450.0 171.12 180.55 169.80
1 6/11/2024 170.66 64761930.0 173.92 174.75 167.41
2 6/10/2024 173.79 50869680.0 176.06 178.57 173.17
3 6/7/2024 177.48 56244930.0 176.13 179.35 175.58
4 6/6/2024 177.94 69887020.0 174.60 179.73 172.73
.. ... ... ... ... ... ...
121 12/18/2023 252.08 116416500.0 253.78 258.74 251.36
122 12/15/2023 253.50 135932800.0 251.21 254.13 248.30
123 12/14/2023 251.05 160829200.0 241.22 253.88 240.79
124 12/13/2023 239.29 146286300.0 234.19 240.30 228.20
125 12/12/2023 237.01 95328310.0 238.55 238.99 233.87
[126 rows x 6 columns]
## Here, I checked for any possible missing values, since when saving, there could be data lost due to the format of the documents.
data['Date'] = pd.to_datetime(data['Date'])
print(data.isnull().sum())
print(data.describe())
print(data.info())
Date 0
Close/Last 0
Volume 0
Open 0
High 0
Low 0
dtype: int64
Date Close/Last Volume Open High Low
count 126 126.00 126.00 126.00 126.00 126.00
mean 2024-03-13 09:20:00 191.54 98652550.56 191.70 195.12 188.08
min 2023-12-12 00:00:00 142.05 50869680.00 140.56 144.44 138.80
25% 2024-01-29 06:00:00 174.14 81622607.50 173.64 176.38 170.96
50% 2024-03-13 12:00:00 180.06 96402245.00 182.05 184.59 177.25
75% 2024-04-28 06:00:00 201.52 111163200.00 201.68 205.09 198.39
max 2024-06-12 00:00:00 261.44 243869700.00 263.66 265.13 257.52
std NaN 28.21 27664733.79 28.56 28.53 28.11
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 126 entries, 0 to 125
Data columns (total 6 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Date 126 non-null datetime64[ns]
1 Close/Last 126 non-null float64
2 Volume 126 non-null float64
3 Open 126 non-null float64
4 High 126 non-null float64
5 Low 126 non-null float64
dtypes: datetime64[ns](1), float64(5)
memory usage: 6.0 KB
None
2 Most Basic Descriptions of the Dataset
Here, I analyze the most basic concept to prepare for further analysis later on
## Here, I will analyze from the basic concept: the main descriptive information of the dataset
summary = data[['Close/Last', 'Volume', 'Open', 'High', 'Low']].describe()
# Display summary statistics
print("Summary Statistics:")
print(summary)
## Here, we have the most basic information about the stock price of Tesla from the most recent six months. However, it would not have any use for us
## when analyzing price. I can still tell from the statistics that in the recent six months, the average price of Tesla is $191, ranging between the
## interval [142.05,261.44]
Summary Statistics:
Close/Last Volume Open High Low
count 126.00 126.00 126.00 126.00 126.00
mean 191.54 98652550.56 191.70 195.12 188.08
std 28.21 27664733.79 28.56 28.53 28.11
min 142.05 50869680.00 140.56 144.44 138.80
25% 174.14 81622607.50 173.64 176.38 170.96
50% 180.06 96402245.00 182.05 184.59 177.25
75% 201.52 111163200.00 201.68 205.09 198.39
max 261.44 243869700.00 263.66 265.13 257.52
# Median for numeric columns
medians = data[['Close/Last', 'Volume', 'Open', 'High', 'Low']].median()
# Display medians
print("\nMedians:")
print(medians)
# Variance
variance = data[['Close/Last', 'Volume', 'Open', 'High', 'Low']].var()
# Standard deviation
std_dev = data[['Close/Last', 'Volume', 'Open', 'High', 'Low']].std()
# Display variance
print("\nVariance:")
print(variance)
# Display standard deviation
print("\nStandard Deviation:")
print(std_dev)
Medians:
Close/Last 180.06
Volume 96402245.00
Open 182.05
High 184.59
Low 177.25
dtype: float64
Variance:
Close/Last 795.98
Volume 765337495676689.88
Open 815.68
High 813.88
Low 790.04
dtype: float64
Standard Deviation:
Close/Last 28.21
Volume 27664733.79
Open 28.56
High 28.53
Low 28.11
dtype: float64
3 Linear Regression on Price and Volume
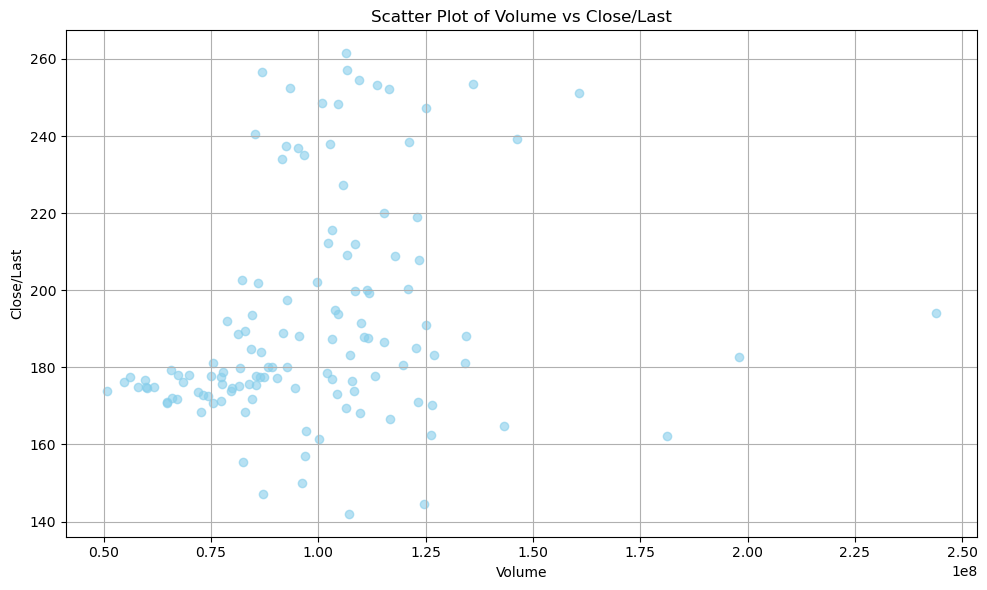
I apply Linear Regression here to explore the relationship between the Price and the Volume of Tesla Stocks, since one of the commonly known pattern is that the Volume confirms price and then the price goes up further. I plan to prove this and see if it happens on Tesla as well. Therefore, I have the scatter plot of the Price and Volume of Tesla. One thing to mention here is that I intentionally put Price on the y-axis so that it will be easier to see, and I view Volume here as a independent variable, when Price is treated as the dependent variable.
# Scatter plot of Volume vs Close/Last
plt.figure(figsize=(10, 6))
plt.scatter(data['Volume'], data['Close/Last'], color='skyblue', alpha=0.6)
plt.title('Scatter Plot of Volume vs Close/Last')
plt.xlabel('Volume')
plt.ylabel('Close/Last')
plt.grid(True)
plt.tight_layout()
plt.show()
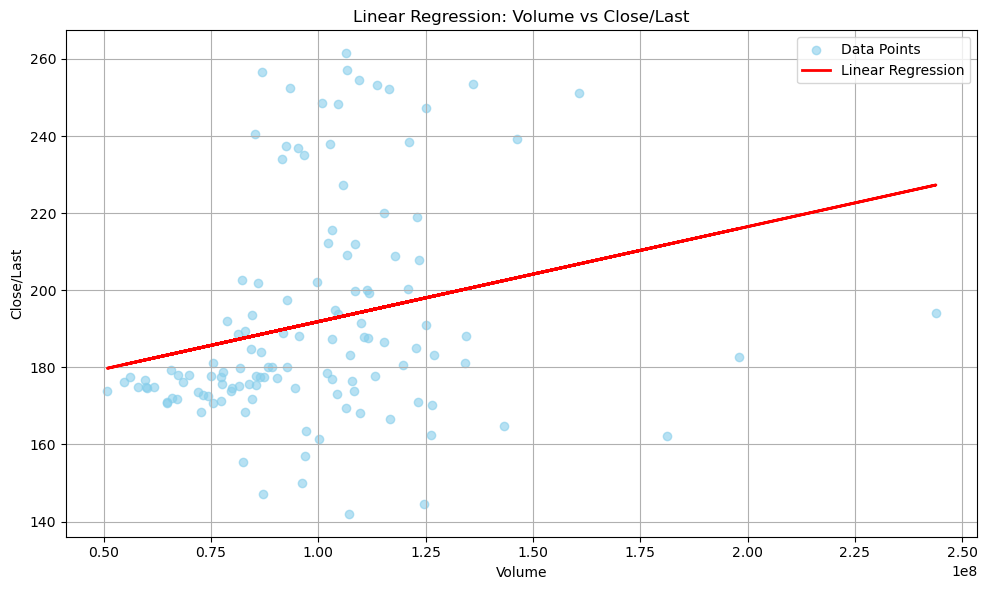
Linear Regression
After the visualization, it is clear that they are linearly related. As the Volume goes up, most of the time the Price goes up as well. However, the slope is not influential or obvious enough for me to utilize this pattern.
# Define X and y
X = data['Volume']
y = data['Close/Last']
# Add a constant for the intercept
X = sm.add_constant(X)
# Fit the linear regression model
model = sm.OLS(y, X)
results = model.fit()
# Visualizing the Linear Regression
plt.figure(figsize=(10, 6))
plt.scatter(data['Volume'], data['Close/Last'], color='skyblue', alpha=0.6, label='Data Points')
plt.plot(data['Volume'], results.predict(X), color='red', linewidth=2, label='Linear Regression')
plt.title('Linear Regression: Volume vs Close/Last')
plt.xlabel('Volume')
plt.ylabel('Close/Last')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
4 K-NN Classification on the Dataset
# Create a new column 'Target' based on the change in 'Close/Last'
data['Target'] = (data['Close/Last'].shift(-1) >= data['Close/Last']).astype(int)
# Drop rows with NaN values (last row where there's no next day data)
data.dropna(inplace=True)
# Separate (X) and (y)
X = data[['Volume']] # Features: Only using 'Volume' as an example
y = data['Target'] # Target: 'Target' column indicating price increase or decrease
# Split data into training and testing
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
k = 5 # Example value of K
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
print("Confusion Matrix:\n", confusion_matrix(y_test, y_pred))
print("\nClassification Report:\n", classification_report(y_test, y_pred))
Confusion Matrix:
[[ 4 16]
[ 8 10]]
Classification Report:
precision recall f1-score support
0 0.33 0.20 0.25 20
1 0.38 0.56 0.45 18
accuracy 0.37 38
macro avg 0.36 0.38 0.35 38
weighted avg 0.36 0.37 0.35 38
It seems like the precision and accuracy of K-NN Classifier on Tesla dataset does not work very well. The percentage is low, and that it is useless to calculate hte Price using K-NN Classifier.
5 Reference: The dataset is downloaded from https://www.nasdaq.com/market-activity/stocks/tsla/historical?page=13&rows_per_page=10&timeline=m6