Methods for Analyzing the Best NBA Players#
Course Project, UC Irvine, Math 10 S24#
I would like to post my notebook on the course’s website. Yes#
Introduction#
In the NBA, many different fans of the game have differing opinions on who the best NBA players are. In this project I intend to show methods on determning who the best NBA players are in terms of scoring output, field goal percentage, and more. I found these stats through a Kaggle dataset that contained these average statistics for the 2023-2024 NBA regular season.
import numpy as np
import pandas as pd
import statistics
import matplotlib.pyplot as plt
import seaborn as sns
import altair as alt
from sklearn.linear_model import LinearRegression
import plotly.express as px
from sklearn.neighbors import KNeighborsRegressor
Altair Plots#
df = pd.read_csv("NBA_2024_per_game(03-01-2024).csv")
df = df.dropna()
c1 = alt.Chart(df).mark_circle().encode(x = alt.X("MP"),
y = alt.X("PTS"),
color = "Pos",
tooltip = ["Player","PTS", "AST", "TRB", "STL", "BLK"])
filtered_PTS = df[df['PTS'] > 20]
filtered_PTS
c2 = alt.Chart(filtered_PTS).mark_circle().encode(x = alt.X("MP", scale = alt.Scale(domain = (28,38))),
y = alt.X("PTS", scale = alt.Scale(domain = (20,36))),
color = "Pos",tooltip = ["Player","PTS", "AST", "TRB", "STL", "BLK"])
c1 | c2
/Users/elijahhornbeak/Downloads/anaconda3/lib/python3.11/site-packages/altair/utils/core.py:395: FutureWarning:
the convert_dtype parameter is deprecated and will be removed in a future version. Do ``ser.astype(object).apply()`` instead if you want ``convert_dtype=False``.
/Users/elijahhornbeak/Downloads/anaconda3/lib/python3.11/site-packages/altair/utils/core.py:395: FutureWarning:
the convert_dtype parameter is deprecated and will be removed in a future version. Do ``ser.astype(object).apply()`` instead if you want ``convert_dtype=False``.
/Users/elijahhornbeak/Downloads/anaconda3/lib/python3.11/site-packages/altair/utils/core.py:395: FutureWarning:
the convert_dtype parameter is deprecated and will be removed in a future version. Do ``ser.astype(object).apply()`` instead if you want ``convert_dtype=False``.
/Users/elijahhornbeak/Downloads/anaconda3/lib/python3.11/site-packages/altair/utils/core.py:395: FutureWarning:
the convert_dtype parameter is deprecated and will be removed in a future version. Do ``ser.astype(object).apply()`` instead if you want ``convert_dtype=False``.
Using Altair I was able to plot a grpah using the minutes played and points per game as the x and y-axis respectively. I also used the tooltip function within altair so that each individual point will have the players name in addition to other stats that are relavent. This is just a way to visualize the trend of minutes played and points per game. The second chart is a chart of the NBA players that scored more than 20 points per game. I also changed the bound of the x and y-axis to centralize the data better.
Linear Regression Model and \(R^2\) Value#
df = pd.DataFrame(df)
df = df[df['PTS'] > 20]
Y = df['PTS'].values
X = df['MP'].values.reshape(-1,1)
model = LinearRegression()
model.fit(X, Y)
Y_pred = model.predict(X)
plt.scatter(X, Y, color='blue', label='NBA Players')
plt.plot(X, Y_pred, color='red', label='Line of best fit')
plt.xlabel('Minutes')
plt.ylabel('Points')
plt.title('Linear Regression')
plt.legend()
plt.show()
r_squared = model.score(X, Y)
print(f'R^2 value: {r_squared}')
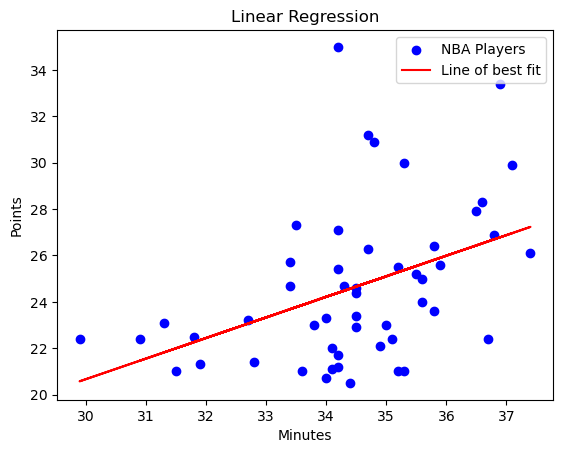
R^2 value: 0.1804183428580789
This Linear Regression plot is using the two variables of minutes on the x-axis and points along the y-axis. I also included the \(R^2\) value of the graph. The low \(R^2\) value shows that the prediction of points based on minutes played is not a great one. A consequence of this is that you can see the players that are above this line, meaning the data points above the line of best fit score more on average based on the amount of minutes they play per game. You can say that these players are above average scorers for the amount of minutes they play. It also shows that there is not a clear relation between points per game and minutes played.
above_average_scorers = df['PTS'] > Y_pred
Players_above_average = df[above_average_scorers]
print("Players that are above average scorers:")
print(Players_above_average)
Players that are above average scorers:
Player Pos Age Tm G GS MP FG FGA FG% \
11 Giannis Antetokounmpo PF 29 MIL 32 32 34.8 11.5 18.9 0.606
25 LaMelo Ball PG 22 CHO 15 15 33.4 8.8 19.9 0.443
58 Devin Booker PG 27 PHO 24 24 35.8 8.9 19.1 0.466
113 Stephen Curry PG 35 GSW 30 30 33.5 8.6 19.0 0.453
125 Luka Dončić PG 24 DAL 31 31 36.9 11.4 23.6 0.484
131 Kevin Durant PF 35 PHO 28 28 37.1 10.4 19.7 0.525
134 Anthony Edwards SG 22 MIN 29 29 34.7 9.0 19.7 0.458
137 Joel Embiid C 29 PHI 25 25 34.2 11.8 21.8 0.540
147 De'Aaron Fox PG 26 SAC 25 25 35.3 10.5 21.8 0.483
161 Shai Gilgeous-Alexander PG 25 OKC 30 30 34.7 11.2 20.6 0.546
181 Tyrese Haliburton PG 23 IND 29 29 34.3 8.8 17.6 0.501
222 Kyrie Irving SG 31 DAL 18 18 31.8 8.4 18.0 0.469
231 LeBron James PF 39 LAL 31 31 34.2 9.4 17.6 0.535
242 Nikola Jokić C 28 DEN 34 34 33.4 9.9 17.8 0.559
263 Kyle Kuzma PF 28 WAS 32 32 31.3 8.9 19.2 0.466
275 Damian Lillard PG 33 MIL 31 31 35.2 7.4 17.1 0.431
293 Lauri Markkanen PF 26 UTA 24 24 32.7 8.0 16.3 0.487
329 Donovan Mitchell SG 27 CLE 24 24 36.5 9.8 21.3 0.457
438 Anfernee Simons SG 24 POR 11 11 34.2 9.5 20.7 0.456
459 Jayson Tatum PF 25 BOS 30 30 36.8 9.3 19.6 0.474
466 Cam Thomas SG 22 BRK 24 20 29.9 8.3 18.6 0.448
527 Zion Williamson PF 23 NOP 27 27 30.9 8.8 15.1 0.582
534 Trae Young PG 25 ATL 30 30 36.6 8.8 20.2 0.436
... FT% ORB DRB TRB AST STL BLK TOV PF PTS
11 ... 0.676 2.7 8.6 11.3 5.7 1.3 1.2 3.8 2.9 30.9
25 ... 0.857 1.5 3.9 5.5 8.2 1.4 0.3 3.9 3.5 24.7
58 ... 0.883 0.9 4.4 5.3 7.9 0.8 0.4 2.8 3.3 26.4
113 ... 0.931 0.5 3.9 4.4 4.5 0.7 0.4 3.1 1.8 27.3
125 ... 0.785 0.8 7.5 8.3 9.4 1.4 0.6 4.0 1.7 33.4
131 ... 0.874 0.4 5.9 6.3 6.0 0.9 1.1 3.4 1.8 29.9
134 ... 0.842 0.6 4.8 5.3 5.1 1.3 0.7 3.3 1.8 26.3
137 ... 0.893 2.8 8.9 11.7 6.0 1.2 2.0 3.8 2.8 35.0
147 ... 0.720 1.0 3.6 4.6 6.1 1.6 0.4 2.6 2.7 30.0
161 ... 0.916 0.8 4.8 5.7 6.3 2.6 0.8 2.0 2.3 31.2
181 ... 0.856 0.7 3.5 4.2 12.7 1.0 0.6 2.6 1.1 24.7
222 ... 0.889 0.6 3.6 4.2 5.1 1.1 0.3 1.3 1.9 22.5
231 ... 0.749 0.9 6.5 7.4 7.4 1.4 0.7 3.3 1.1 25.4
242 ... 0.818 3.0 9.2 12.3 9.1 1.1 0.9 2.7 2.6 25.7
263 ... 0.768 0.9 5.3 6.2 4.3 0.3 0.6 2.6 2.2 23.1
275 ... 0.924 0.6 3.9 4.5 6.8 1.0 0.2 2.7 1.7 25.5
293 ... 0.861 2.3 6.2 8.5 1.6 1.0 0.6 1.2 2.1 23.2
329 ... 0.895 1.1 4.6 5.7 5.7 1.9 0.5 2.6 2.4 27.9
438 ... 0.923 0.6 2.5 3.1 5.3 0.9 0.1 2.4 2.0 27.1
459 ... 0.806 0.9 7.5 8.4 4.4 1.0 0.5 2.9 2.1 26.9
466 ... 0.806 0.3 2.3 2.6 2.3 0.6 0.4 1.7 2.2 22.4
527 ... 0.656 2.0 4.2 6.1 4.6 1.0 0.3 2.6 2.7 22.4
534 ... 0.860 0.5 2.5 3.0 11.3 1.4 0.2 4.3 2.0 28.3
[23 rows x 29 columns]
The 23 NBA players mentioned abpove score at a higher output than the liner model predicted based on their minutes per game. There are a lot that make sense, but there are a few NBA players that many consider to not be that good such as Kyle Kuzma and Cam Thomas. Those are the players that surprised me who were above average scorers from the minutes that they played.
below_average_scorers = df['PTS'] <= Y_pred
Players_below_average = df[below_average_scorers]
print("Players that are below average scorers:")
print(Players_below_average)
Players that are below average scorers:
Player Pos Age Tm G GS MP FG FGA FG% ... \
3 Bam Adebayo C 26 MIA 23 23 34.1 8.0 15.7 0.506 ...
27 Paolo Banchero PF 21 ORL 32 32 34.2 7.8 16.8 0.465 ...
28 Desmond Bane SG 25 MEM 31 31 34.5 9.0 19.2 0.471 ...
32 Scottie Barnes SG 22 TOR 33 33 35.2 7.8 16.3 0.480 ...
65 Mikal Bridges SF 27 BRK 33 33 34.1 7.5 16.4 0.457 ...
74 Jaylen Brown SF 27 BOS 30 30 33.8 8.9 18.2 0.489 ...
78 Jalen Brunson PG 27 NYK 33 33 35.9 9.0 19.4 0.463 ...
84 Jimmy Butler PF 34 MIA 24 24 33.6 6.5 14.0 0.464 ...
111 Cade Cunningham PG 22 DET 33 33 35.0 8.5 19.2 0.443 ...
115 Anthony Davis C 30 LAL 32 32 35.6 9.5 17.2 0.551 ...
119 DeMar DeRozan SF 34 CHI 32 32 36.7 7.8 17.0 0.455 ...
152 Darius Garland PG 24 CLE 20 20 34.0 7.6 16.1 0.470 ...
157 Paul George PF 33 LAC 30 30 34.5 8.0 17.7 0.451 ...
170 Jerami Grant PF 29 POR 28 28 34.9 7.5 16.4 0.459 ...
200 Tyler Herro SG 24 MIA 15 15 34.5 8.7 19.1 0.455 ...
221 Brandon Ingram SF 26 NOP 30 30 34.0 8.8 17.5 0.501 ...
228 Jaren Jackson Jr. C 24 MEM 32 32 31.5 7.2 15.6 0.458 ...
266 Zach LaVine SG 28 CHI 18 18 35.3 7.3 16.6 0.443 ...
270 Kawhi Leonard SF 32 LAC 28 28 34.5 9.1 17.4 0.522 ...
303 Tyrese Maxey PG 23 PHI 31 31 37.4 9.0 19.7 0.458 ...
336 Ja Morant PG 24 MEM 6 6 35.5 9.3 20.0 0.467 ...
340 Dejounte Murray SG 27 ATL 32 32 34.4 7.9 17.1 0.461 ...
397 Julius Randle PF 29 NYK 33 33 35.6 8.7 18.3 0.474 ...
414 Terry Rozier SG 29 CHO 20 20 35.8 8.7 18.8 0.463 ...
429 Alperen Şengün C 21 HOU 31 31 31.9 8.4 15.4 0.544 ...
436 Pascal Siakam PF 29 TOR 33 33 35.1 8.5 16.4 0.518 ...
477 Karl-Anthony Towns PF 28 MIN 31 31 32.8 7.7 15.1 0.509 ...
494 Franz Wagner SF 22 ORL 32 32 34.2 7.8 16.8 0.465 ...
FT% ORB DRB TRB AST STL BLK TOV PF PTS
3 0.777 2.1 8.3 10.4 4.0 1.1 1.0 2.7 2.4 22.0
27 0.697 1.2 5.8 7.0 4.7 1.0 0.6 3.1 2.0 21.7
28 0.858 0.9 3.7 4.6 5.2 1.1 0.6 2.8 2.9 24.6
32 0.772 2.6 6.7 9.3 5.8 1.5 1.4 2.4 2.0 21.0
65 0.829 1.0 4.3 5.3 3.8 0.9 0.4 2.3 1.6 21.1
74 0.733 0.9 4.2 5.1 3.7 1.1 0.6 2.5 2.7 23.0
78 0.820 0.7 3.3 4.0 6.2 1.1 0.2 2.4 2.2 25.6
84 0.881 1.9 3.2 5.0 4.5 1.0 0.4 1.8 1.1 21.0
111 0.870 0.5 3.5 4.0 7.3 1.0 0.3 3.9 2.8 23.0
115 0.806 3.3 9.0 12.3 3.3 1.2 2.6 2.0 2.6 25.0
119 0.838 0.7 3.2 3.8 5.4 1.1 0.8 1.4 2.2 22.4
152 0.835 0.6 2.2 2.8 5.9 1.6 0.2 3.8 1.6 20.7
157 0.931 0.7 4.8 5.5 4.0 1.6 0.3 2.3 3.0 22.9
170 0.810 0.7 3.2 3.9 2.6 0.7 0.8 2.4 2.3 22.1
200 0.872 0.6 4.9 5.5 4.5 1.3 0.1 2.7 1.3 23.4
221 0.815 0.7 4.1 4.8 5.5 0.8 0.5 2.6 2.2 23.3
228 0.832 1.4 4.2 5.5 1.7 0.8 1.6 1.9 3.6 21.0
266 0.866 0.3 4.6 4.9 3.4 0.9 0.2 2.0 2.1 21.0
270 0.872 1.1 4.9 5.9 3.6 1.6 0.7 1.5 1.4 24.4
303 0.873 0.5 3.2 3.8 6.5 0.8 0.5 1.5 2.1 26.1
336 0.829 0.5 4.5 5.0 7.8 0.7 0.7 3.2 2.0 25.2
340 0.817 0.8 3.8 4.6 5.2 1.5 0.3 2.1 1.7 20.5
397 0.763 2.2 7.4 9.6 4.7 0.5 0.2 3.4 2.8 24.0
414 0.854 0.6 3.3 3.9 7.2 1.2 0.4 2.4 1.8 23.6
429 0.728 2.6 6.5 9.1 5.3 1.1 0.8 2.5 3.3 21.3
436 0.749 1.5 5.1 6.5 5.0 0.8 0.2 2.2 2.3 22.4
477 0.895 1.6 7.5 9.2 2.9 0.8 0.5 3.0 3.5 21.4
494 0.847 1.1 4.9 6.0 4.0 1.2 0.4 1.8 2.3 21.2
[28 rows x 29 columns]
These 28 NBA players are those who scored less than the model predicted, many of which made the All-Star game this year or were on the All-NBA teams, such as Scottie Barnes, Jalen Brunson, Kawhi Leonard, Anthony Davis, and Jaylen Brown to name a few. I believe that this shows that basing the quality of a player cannot only be determined through their points per game output based on minutes played and how above average they are.
Plotly Component#
We will now use a bar chart to visualize the average points per game for the NBA players that average 25 points per game or more.
df_PPG = df[df['PTS'] >= 25]
PPG = pd.DataFrame(df_PPG.groupby('Player')['PTS'].mean())
bar_chart = px.bar(df_PPG, x = PPG.index, y = PPG["PTS"])
bar_chart.show()
I will create another barchart but now will have the NBA players that average a higher field goal percentage than 50%.
df_FG = df[df['FG%'] > 0.500]
FG = pd.DataFrame(df_FG.groupby('Player')['FG%'].mean())
bar_chart = px.bar(df_FG, x = FG.index, y = FG["FG%"])
bar_chart.show()
When looking at both of the bar charts, you can see some overlap in both charts with the same players such as Anthony Davis, Giannis Antetokounmpo, Joel Embiid, Kevin Durant, LeBron James, Nikola Jokić, and Shai Gilgeous-Alexander. These are the best scorers in the NBA who are the most efficient when shooting the ball.
Correlation between the Five Main Stats and FG% and MP#
corr_df = df_PPG[['PTS', 'TRB', 'AST', 'STL', 'BLK', 'FG%', 'MP' ]]
corr_df.corr()
| PTS | TRB | AST | STL | BLK | FG% | MP | |
|---|---|---|---|---|---|---|---|
| PTS | 1.000000 | 0.273783 | 0.112722 | 0.407189 | 0.252402 | 0.346648 | 0.042197 |
| TRB | 0.273783 | 1.000000 | -0.151427 | 0.070361 | 0.797259 | 0.810272 | -0.254707 |
| AST | 0.112722 | -0.151427 | 1.000000 | 0.057256 | -0.361143 | -0.144822 | 0.150785 |
| STL | 0.407189 | 0.070361 | 0.057256 | 1.000000 | 0.071895 | 0.288845 | -0.037373 |
| BLK | 0.252402 | 0.797259 | -0.361143 | 0.071895 | 1.000000 | 0.697845 | -0.133159 |
| FG% | 0.346648 | 0.810272 | -0.144822 | 0.288845 | 0.697845 | 1.000000 | -0.328815 |
| MP | 0.042197 | -0.254707 | 0.150785 | -0.037373 | -0.133159 | -0.328815 | 1.000000 |
For this correlation matrix, I used the NBA players that score more than 25 points per game. From the correlation matrix you can see that there is a somewhat large correlation shared between assist and blocks. This means that the higher assist the less likely you are to have higher blocks and vice versa. This most likely stems from Centers being the ones who get the most blocks, but they also tend to get fewer assist. There is a very high positive correlation between blocks and total rebounds as well as field goal percentage and total rebounds. This is also most likely due to Center and Power Forwards since they tend to be closer to the basket (higher field goal percentage) and taller players (higher rebounds and blocks).
Centers and Outliers#
In the NBA the Center is usually the player that has the most rebounds per game, blocks, and can score a bit but not much else. We will now see of there are Centers that completely break that idea.
kNN Regression#
df = pd.read_csv("NBA_2024_per_game(03-01-2024).csv")
df = df.dropna()
df_center = df[df['Pos'] == 'C']
X = df_center['TRB'].values.reshape(-1,1)
y = df_center['AST'].values
knn = KNeighborsRegressor(n_neighbors=12)
knn.fit(X, y)
X_test = np.arange(0,15,0.5).reshape(-1,1)
y_pred = knn.predict(X_test)
plt.scatter(X, y, color='darkorange', label='data')
plt.plot(X_test, y_pred, color='navy', label='KNN regression')
plt.xlabel('Rebounds per game')
plt.ylabel('Assist per game')
plt.title('KNN Regression Plot')
plt.legend()
plt.show()
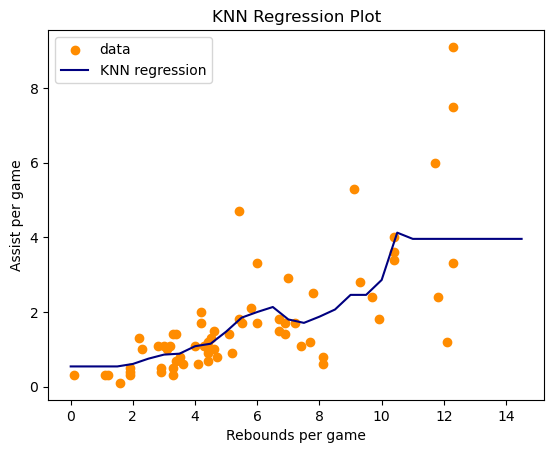
Using the k-nearest-neighbors regression plot, you can see that there is a trend for a majority of the Centers in the NBA, but there are also quite a few outliers. I chose the y-axis to be assist per game since Centers are not known for their assists, but there are quite a few centers who had more than 5 assist per game. The biggest outliers are players such as Nikola Jokić, Domantis Sabonis, and Joel Embiid. The k-nearest-neighbors regression plot can predict the trend of rebounds per game to assist per game, but the three aforementioned Centers are outliers and elite passers at their position.