Sleep, Exercise, and UCI Life’s Effect on a College Student’s Health#
Name: Alex Kimm#
Course Project, UC Irvine, Math 10, S24#
ID: 26177943#
Yes, I would like to post my notebook on the course’s website.#
This project will be based on several statistics that my Fitbit Versa 4 has collected over the a period of over a year, as well as external data that I manually input into a spreadsheet.
My watch collects several different types of statistics, but this project will focus specifically on data relating to my sleep and exercise. I had to divide the work into separate CSVs to maintain readability and because sleep and exercise data tracked by the watch do not have compatible time logs. Later in the project, I will combine the data later to make more interesting discoveries.
I preemtively load all these libraries here for simplicity, but every time I need to use them, I reload them again for the sake of readability.
import pandas as pd
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
from datetime import datetime, timedelta
from itertools import combinations
from sklearn.linear_model import LinearRegression, Ridge, Lasso, LogisticRegression
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
from pandas.plotting import scatter_matrix
import tensorflow as tf
from tensorflow.keras.models import Sequential, load_model
from tensorflow.keras.layers import Dense
from sklearn.metrics import accuracy_score
2024-06-11 21:57:40.529274: I tensorflow/core/platform/cpu_feature_guard.cc:210] This TensorFlow binary is optimized to use available CPU instructions in performance-critical operations.
To enable the following instructions: AVX2 FMA, in other operations, rebuild TensorFlow with the appropriate compiler flags.
The first thing I had to do after importing all the necessary libraries was take inventory of what I had in my dataframe. Firstly, the raw csv file was formatted very peculiarly. Every element was a string, which meant I had to manually (utilizing Ctrl + F) replace every of these entries and replace them with a format that I could actually work with. For example, for working with any numerical data, I would need either ints or floats.
In addition, when Python is compiling CSVs into data, it automatically assumes data in a format that it does not recognize as a string. This would normally be acceptable, but since I have dates and times, it would be advantageous to convert these strings into Python datetime objects.
import pandas as pd
import numpy as np
import seaborn as sns
from datetime import datetime, timedelta
# Create a dataframe of sleep data without any missing data.
df_sleep = pd.read_csv('sleep.csv')
df_sleep.dropna(inplace=True)
df_sleep = df_sleep.reset_index(drop=True)
# As mentioned before, I needed to change the dates as datetime objects in Python.
df_sleep['Start Time'] = pd.to_datetime(df_sleep['Start Time'], errors='coerce')
df_sleep['End Time'] = pd.to_datetime(df_sleep['End Time'], errors='coerce')
# It is helpful to not only see when my sleep started and ended, as well as how much that duration was.
df_sleep['Hours Asleep'] = (df_sleep['End Time'].astype(int) - df_sleep['Start Time'].astype(int)).div(10**9).div(3600)
# Must divide by 10e9 because astype returns the datetimes in nanoseconds
It may not look like it, but getting the df_sleep dataframe to accept dates instead of just the default of strings took nearly an hour. The documentation for the python data type datetime was dense and unclear to me, someone who has never worked with that module before. I originally tried using the .apply() function in pandas, but it did not work with datetimes since .apply() works on the entire column of a dataframe and datetimes work with individual strings only.
We now repeat this same process for exercise data.
# Create an dataframe of exercise data.
df_exercise = pd.read_csv("exercise.csv")
df_exercise['Date'] = pd.to_datetime(df_exercise['Date'], errors='coerce')
df_exercise.dropna(inplace=True)
Currently, my sleep and exercise data are separated into two dataframes. I think that there are some very interesting questions to be had about whether certain parts of my exercise affect parts of the type of sleep I get. To find out, I must have to combine the two dataframe into one massive dataframe with over 15 features.
There are, however, a few problems.
On some days I wore my watch while I slept but not while I went about my daily activities that day (and vice versa). This means that the time data in my exercise and sleep dataframes are different lengths.
The nature of the sleep dataframe is that it keeps track of when I fall asleep and when I wake up, which are two different days…sometimes. This is because, against my doctor’s wishes, I frequently sleep after 12 AM and my watch keeps track of my naps as well, meaning there are duplicate dates. This necessitates that I find a way to describe how much sleep I get at night only.
I am given the choice of pairing my exercise with the sleep of the night before or the night after, which fundamentally asks different questions. If I choose to look at exercise and the same night’s sleep, then my data is framed to answer “How do my exercise habits affect my sleep?”, whereas looking at the previous night’s sleep and the activity the next day asks “How does my sleep affect my exercise?”. I personally think that looking at how my sleep is affected by the day’s exercise will be more interesting insight.
If I want to combine my data, I need to manipulate both dataframes because sleep datetimes are given with precision to the second, while exercise datetimes are given with precision to the day.
I will be resolving all of the issues in the following code blocks.
# Create a new column that keeps track of which day my sleep belongs (problem 2).
df_sleep['Date'] = df_sleep['Start Time']
# If I sleep and wake up on the same day, then that counts as the previous day's sleep.
# Otherwise, it is safe to say that it is the same day.
for i in range(0, len(df_sleep)):
if df_sleep['Start Time'][i].date() == df_sleep['End Time'][i].date():
df_sleep.loc[i,'Date'] = df_sleep['Start Time'][i].date() - timedelta(days = 1)
else:
df_sleep.loc[i, 'Date'] = df_sleep['Start Time'][i].date()
# Ensure that the entire column is not changed to the general dataframe "object" and instead "datetime".
df_sleep = df_sleep.astype({"Date": "datetime64[ns]"})
/var/folders/fw/7zvj6rks73qb1bvpcbz39q6c0000gn/T/ipykernel_5223/3482543601.py:8: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise an error in a future version of pandas. Value '2024-05-29' has dtype incompatible with datetime64[ns], please explicitly cast to a compatible dtype first.
df_sleep.loc[i,'Date'] = df_sleep['Start Time'][i].date() - timedelta(days = 1)
However, on days where I both take a nap during the day, there is a chance that that day is rolled back to the previous day. However, this is not an issue for reasons that will be addressed in a subsequent code block.
# Create a new set of columns to add matching dates from the exercise and sleep dataframes.
df_exercise_features = ["Calories Burned", "Steps", "Distance", "Floors", "Minutes Sedentary",
"Minutes Lightly Active", "Minutes Fairly Active", "Minutes Very Active",
"Activity Calories"]
# Make a new dataframe out of those columns.
df_exercise_2 = pd.DataFrame(np.zeros((0,len(df_exercise_features))), columns=df_exercise_features)
# Filter for the same date, then add them to the new exercise dataframe.
for i in range(1, len(df_sleep)):
for j in range(1, len(df_exercise)):
if df_sleep['Date'][i] == df_exercise['Date'][j]:
df_exercise_2 = df_exercise_2._append(df_exercise.iloc[j], ignore_index=True)
Now repeat a similar process for the sleep dataframe to remove excessive data in the form of naps. This is done by taking advantage of the fact that sleep.csv lists days in reverse chronological order. Thus, any groups of sleep that occur on the same day will have the first occurrence (which will take place later, at night) be chosen.
df_sleep_features = ['Start Time','End Time','Minutes Asleep','Minutes Awake','Number of Awakenings','Time in Bed',
'Minutes REM Sleep','Minutes Light Sleep','Minutes Deep Sleep','Hours Asleep','Date']
df_sleep_2 = pd.DataFrame(np.zeros((0,len(df_sleep_features))), columns=df_sleep_features)
for i in range(1, len(df_sleep)):
if df_sleep['Date'][i] == df_sleep['Date'][i-1]:
continue
else:
df_sleep_2 = df_sleep_2._append(df_sleep.iloc[i-1], ignore_index=True)
# Remove start and end time because they are irrelevant for the time being.
df_sleep_2.drop(columns=['Start Time', 'End Time'], axis=1)
/var/folders/fw/7zvj6rks73qb1bvpcbz39q6c0000gn/T/ipykernel_5223/2331035335.py:10: FutureWarning: The behavior of DataFrame concatenation with empty or all-NA entries is deprecated. In a future version, this will no longer exclude empty or all-NA columns when determining the result dtypes. To retain the old behavior, exclude the relevant entries before the concat operation.
df_sleep_2 = df_sleep_2._append(df_sleep.iloc[i-1], ignore_index=True)
| Minutes Asleep | Minutes Awake | Number of Awakenings | Time in Bed | Minutes REM Sleep | Minutes Light Sleep | Minutes Deep Sleep | Hours Asleep | Date | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 360.0 | 73.0 | 37.0 | 433.0 | 58.0 | 270.0 | 32.0 | 7.233333 | 2024-05-29 |
| 1 | 296.0 | 42.0 | 29.0 | 338.0 | 36.0 | 183.0 | 77.0 | 5.650000 | 2024-05-28 |
| 2 | 370.0 | 72.0 | 37.0 | 442.0 | 61.0 | 262.0 | 47.0 | 7.366667 | 2024-05-27 |
| 3 | 403.0 | 89.0 | 41.0 | 492.0 | 74.0 | 285.0 | 44.0 | 8.200000 | 2024-05-24 |
| 4 | 185.0 | 26.0 | 18.0 | 211.0 | 34.0 | 121.0 | 30.0 | 3.533333 | 2024-05-23 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 329 | 322.0 | 46.0 | 37.0 | 368.0 | 87.0 | 184.0 | 51.0 | 6.150000 | 2023-03-14 |
| 330 | 426.0 | 60.0 | 53.0 | 486.0 | 118.0 | 227.0 | 81.0 | 8.100000 | 2023-03-13 |
| 331 | 241.0 | 44.0 | 26.0 | 285.0 | 53.0 | 131.0 | 57.0 | 4.750000 | 2023-03-12 |
| 332 | 453.0 | 77.0 | 46.0 | 530.0 | 81.0 | 293.0 | 79.0 | 9.833333 | 2023-03-11 |
| 333 | 453.0 | 106.0 | 60.0 | 559.0 | 96.0 | 290.0 | 67.0 | 9.333333 | 2023-03-10 |
334 rows × 9 columns
Now, we can use our previously collected dataframes containing exercise and sleep data and now combine them into one big dataframe! When we eventually combine the exercise and sleep dataframes, it is important that there isn’t a duplicate date column because that will cause issues when we try to work with that data.
sleep_cols = ['Hours Asleep', 'Minutes Asleep', 'Minutes Awake', 'Number of Awakenings',
'Time in Bed', 'Minutes REM Sleep', 'Minutes Light Sleep', 'Minutes Deep Sleep']
df_sleep_3 = df_sleep_2[sleep_cols]
# Create the dataframe that will house both dataframes' original data.
col=['Date', 'Hours Asleep', 'Minutes Asleep', 'Minutes Awake', 'Number of Awakenings',
'Time in Bed', 'Minutes REM Sleep', 'Minutes Light Sleep', 'Minutes Deep Sleep', 'Calories Burned',
'Steps', 'Distance', 'Floors', 'Minutes Sedentary', 'Minutes Lightly Active', 'Minutes Fairly Active',
'Minutes Very Active', 'Activity Calories']
df = pd.DataFrame(np.zeros((0,len(col))), columns=col)
# If a date is shared between exercise and sleep, then they are added to the new dataframe.
for i in range(len(df_sleep_2)):
for j in range(len(df_exercise_2)):
if df_sleep_2['Date'][i] == df_exercise_2['Date'][j]:
a = pd.concat([df_sleep_3.iloc[i], df_exercise_2.iloc[j]])
df = df._append(a, ignore_index=True)
/var/folders/fw/7zvj6rks73qb1bvpcbz39q6c0000gn/T/ipykernel_5223/3050805482.py:17: FutureWarning: The behavior of DataFrame concatenation with empty or all-NA entries is deprecated. In a future version, this will no longer exclude empty or all-NA columns when determining the result dtypes. To retain the old behavior, exclude the relevant entries before the concat operation.
df = df._append(a, ignore_index=True)
Now, we can finally analyze data among both sleep and exercise data. The first course of action is to create a correlation plot to get a good idea of which variables are most correlated with others.
import seaborn as sns
df_columns = ['Hours Asleep', 'Minutes Asleep', 'Minutes Awake', 'Number of Awakenings',
'Time in Bed', 'Minutes REM Sleep', 'Minutes Light Sleep', 'Minutes Deep Sleep', 'Calories Burned',
'Steps', 'Distance', 'Floors', 'Minutes Sedentary', 'Minutes Lightly Active', 'Minutes Fairly Active',
'Minutes Very Active', 'Activity Calories']
corr = df[df_columns].corr()
obj = sns.heatmap(data=corr, cmap='Purples');
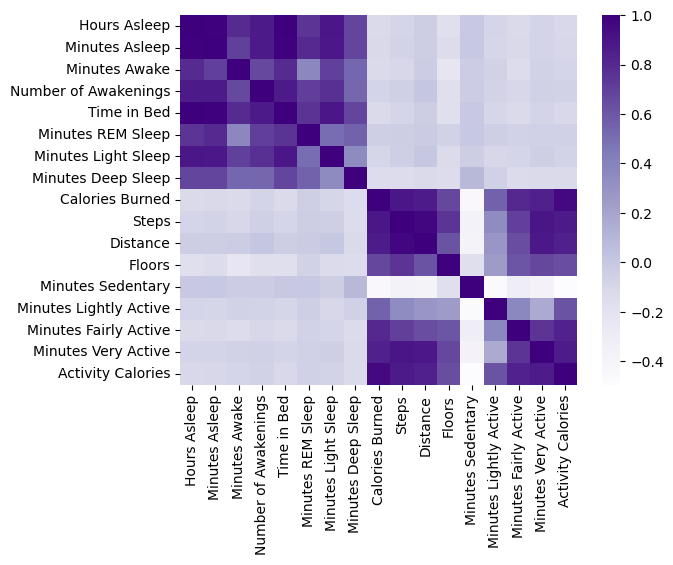
Just visually, it appears that generally the sleep variables have almost no correlation with exercise variables. I am extremely disappointed that there is no deep link. With that said, there is still a wealth of knowledge to be had about how aspects of my exercise relates to itself, as well as how aspects of my sleep relates to itself.
Let’s focus on just sleep for now. Looking at the heatmap, it appears that there is a moderate correlation between the minutes of REM, Light, and Deep Sleep that I get and the Number of Awakenings in one night. However, what if there is some combination of these features that altogether better predict how well I sleep? Firstly, we’ll have to see if I at all meet the benchmark. According to Healthline, the average person should aim to get around 25% REM, 45% Light, 25% Deep Sleep, and 5% Awake/Restless/Very Light. First, let’s observe if this is indeed the case for my sleep.
import matplotlib.pyplot as plt
fig, (ax1, ax2, ax3, ax4) = plt.subplots(1,4)
fig.set_size_inches(10,4,forward=True)
fig.tight_layout()
ax1.hist(df['Minutes REM Sleep'] / df['Minutes Asleep'], color='lightcoral');
ax1.set_title("REM Sleep")
ax1.set_xlabel("Proportion of Total Sleep")
ax1.set_ylabel("Count")
ax2.hist(df['Minutes Light Sleep'] / df['Minutes Asleep'], color='gold');
ax2.set_title("Light Sleep")
ax2.set_xlabel("Proportion of Total Sleep")
ax2.set_ylabel("Count")
ax3.hist(df['Minutes Deep Sleep'] / df['Minutes Asleep'], color='paleturquoise');
ax3.set_title("Deep Sleep")
ax3.set_xlabel("Proportion of Total Sleep")
ax3.set_ylabel("Count")
ax4.hist(df['Minutes Awake'] / df['Minutes Asleep'], color='thistle');
ax4.set_title("Restlessness")
ax4.set_xlabel("Proportion of Total Sleep")
ax4.set_ylabel("Count")
print(f"The mean proportion of REM Sleep is {(df['Minutes REM Sleep'] / df['Minutes Asleep']).mean()}")
print(f"The mean proportion of Light Sleep is {(df['Minutes Light Sleep'] / df['Minutes Asleep']).mean()}")
print(f"The mean proportion of Deep Sleep is {(df['Minutes Deep Sleep'] / df['Minutes Asleep']).mean()}")
print(f"The mean proportion of Restlessness is {(df['Minutes Awake'] / df['Minutes Asleep']).mean()}")
The mean proportion of REM Sleep is 0.19654752855714724
The mean proportion of Light Sleep is 0.6227084642542776
The mean proportion of Deep Sleep is 0.18074400718857522
The mean proportion of Restlessness is 0.17755921760334448
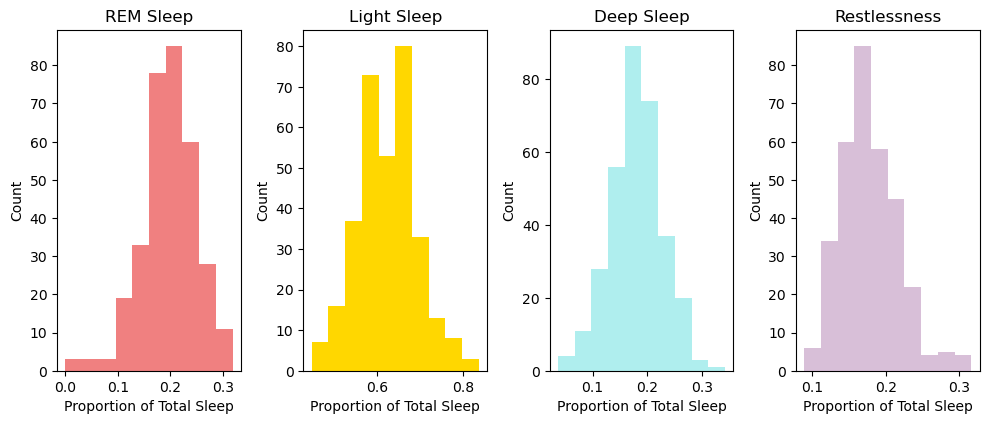
Unfortunately, it seems that I in fact do not get the proper amount of each sleep. Particularly, I am getting too much Light Sleep and Restlessness and too little of both REM and Deep Sleep. This suggests that it takes a while for me to fall asleep, as well as the quality of the sleep that I do get tends to be lower than what I can possibly achieve. This is detrimental to long-term health because REM and Deep Sleep are crucial to the replenishment of cells from the previous day. Essentially, Deep Sleep allows for the body to do its daily cleanup.
Let’s see how well each of these four features affect how many times I wake up during the night.
from itertools import combinations
from sklearn.linear_model import LinearRegression, Ridge, Lasso, LogisticRegression
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
features = ['Minutes Awake', 'Minutes REM Sleep', 'Minutes Light Sleep', 'Minutes Deep Sleep']
combos = []
for i in range(1,len(df_columns)):
combos += combinations(features, i)
combos = [list(combo) for combo in combos]
train_list = []
test_list = []
def predict_calories():
for combo in combos:
lm = LinearRegression()
x_train, x_test, y_train, y_test = train_test_split(df[combo], df['Number of Awakenings'], test_size=0.5, random_state=0)
lm.fit(x_train, y_train)
train_list.append(lm.score(x_train, y_train))
test_list.append(lm.score(x_test, y_test))
predict_calories()
print(f"The best combination of features is {combos[test_list.index(np.max(test_list))]}, with a score of {np.max(test_list)}")
The best combination of features is ['Minutes Awake', 'Minutes REM Sleep', 'Minutes Light Sleep', 'Minutes Deep Sleep'], with a score of 0.7694802190869687
Thus, we conclude the best subset of features to use to predict how many times I wake up per night is the subset that contains all of the Minutes of the Type of Sleep that I get per night. This makes sense, since the number of awakenings should roughly translate to a combined look at how all of my sleep interacts with each other. However, what if a linear model is not the best model for this function? It’s equally possible that there is some more complex polynomial that will match these results better, so let’s explore those possibilities.
We will be using Ridge Regression and Lasso Regression. We must first normalize this data because the penalties for both Ridge and Lasso Regression depend on the magnitude of the coefficients. Larger coefficients from larger data will have greater effects, so we want to minimize this. As a baseline, let’s compare it with a normal Linear Regression model. Note: Linear Model’s performance does not depend on scaling, but we can still use scaled data to receive the same results regarding performance.
alpha = 0.01
features = ["Minutes Awake", "Minutes REM Sleep", "Minutes Light Sleep", "Minutes Deep Sleep", "Number of Awakenings"]
df_scaled = df[features]
for i in features:
col = (df[i] - df[i].mean()) / df[i].std()
df_scaled.loc[:,i] = col
# Linear Regression (X - X')/std(X)
lm = LinearRegression()
kf = KFold(n_splits=5, shuffle=True, random_state=1)
lm_scores = cross_val_score(lm, df[features[0:4]], df[features[4]], cv=kf, scoring='r2')
for i in range(len(lm_scores)):
print(f"Fold {i+1} R^2 score: {lm_scores[i]}")
print()
# Ridge Regression (X - X')/std(X)
ridge = Ridge(alpha=alpha)
kf = KFold(n_splits=5, shuffle=True, random_state=1)
ridge_scores = cross_val_score(ridge, df[features[0:4]], df[features[4]], cv=kf, scoring='r2')
for i in range(len(ridge_scores)):
print(f"Fold {i+1} R^2 score: {ridge_scores[i]}")
print()
# Lasso Regression (X - X')/std(X)
lasso = Lasso(alpha=alpha)
kf = KFold(n_splits=5, shuffle=True, random_state=1)
lasso_scores = cross_val_score(lasso, df[features[0:4]], df[features[4]], cv=kf, scoring='r2')
for i in range(len(lasso_scores)):
print(f"Fold {i+1} R^2 score: {lasso_scores[i]}")
print()
print(f"The mean R^2 value for this Linear Model is: {lm_scores.mean()}.")
print(f"The mean R^2 value for this Ridge Model is: {ridge_scores.mean()}.")
print(f"The mean R^2 value for this Lasso Model is: {lasso_scores.mean()}.")
Fold 1 R^2 score: 0.7715045370093095
Fold 2 R^2 score: 0.7552979419475101
Fold 3 R^2 score: 0.74803283059773
Fold 4 R^2 score: 0.6948217051159891
Fold 5 R^2 score: 0.7907530964553503
Fold 1 R^2 score: 0.7715045352923458
Fold 2 R^2 score: 0.7552979416026261
Fold 3 R^2 score: 0.7480328363765334
Fold 4 R^2 score: 0.6948217024395231
Fold 5 R^2 score: 0.7907530976467543
Fold 1 R^2 score: 0.7714936422629195
Fold 2 R^2 score: 0.7552997471034357
Fold 3 R^2 score: 0.7480446134512566
Fold 4 R^2 score: 0.6948235317103824
Fold 5 R^2 score: 0.7907538024471161
The mean R^2 value for this Linear Model is: 0.7520820222251777.
The mean R^2 value for this Ridge Model is: 0.7520820226715565.
The mean R^2 value for this Lasso Model is: 0.7520830673950221.
We use Ridge and Lasso Regression to avoid overfitting of data, but as it turns out, the Linear Model has similar performance to the other two models.
Obviously, since this data is fourth-dimensional, there really is no good way of representing it in two dimensions without greatly simplifying the information we wish to convey. However, we can create 2-dimensional plots of each combination of data.
from pandas.plotting import scatter_matrix
scatter_matrix(df_scaled, alpha=0.75, figsize=(10, 10), diagonal='kde');
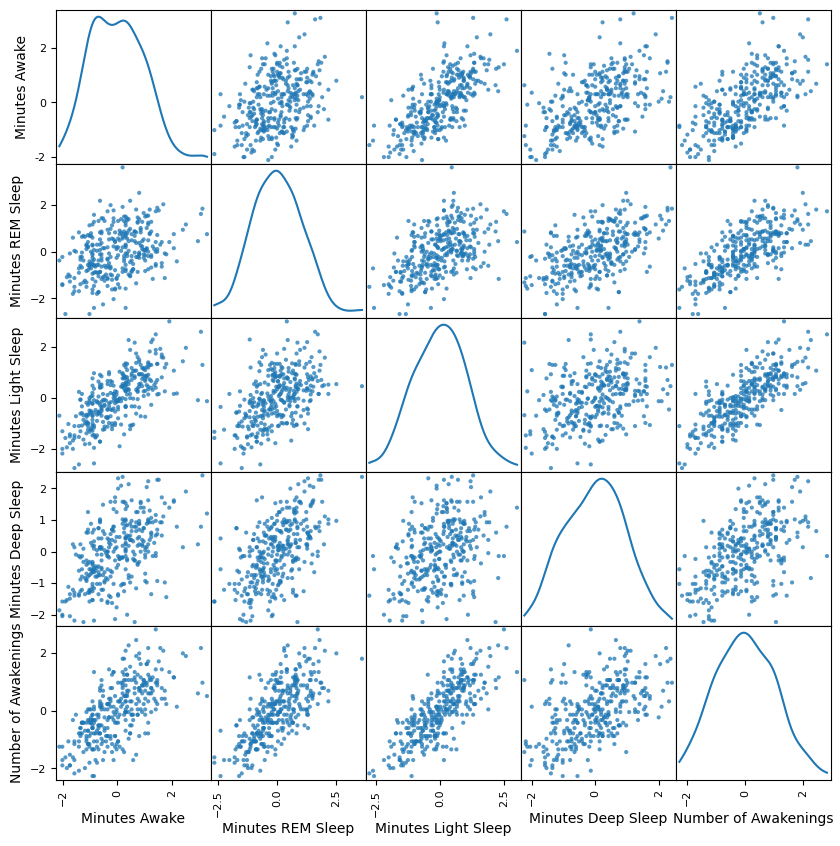
We only really care about the final row, as it shows each combination of the comparisons of each feature against the feature we set out to show, the Number of Awakenings. We can clearly see that for all of them, there is at least a weak to moderate correlation, particular with REM Sleep and Light Sleep.
I have one last CSV file to load into this data science project! However, first, I must start with a short explanation. UCI is known for many things, but perhaps the strangest is a tradition relating to what people call “Petr stickers”, which are stickers drawn as parodies of UCI’s mascot, Peter the Anteater. It is not uncommon to see students run to a certain part of campus from Aldrich after finding out where on campus these stickers are being released.
I have participated in a few of these runs and have kept track of on which days I have collected stickers. Clearly, the physical aspect of running in order to obtain these stickers contributes to my physical exercise of that day, at least in part. I want to use the remainder of this project to see if we can classify days where I do these runs and days where I do not based on my watch’s exercise data.
# Create a new dataframe that has all data with a new "Sticker Received" column for that day.
df['Sticker Received'] = np.full(len(df),False)
df_petr = pd.read_csv("petr.csv")
df_petr = df_petr.drop(labels=['Name', 'Trade Date', 'Traded For', 'Petr', 'Notes', 'Unnamed: 6'],axis=1)
df_petr['Collection Date'] = pd.to_datetime(df_petr['Collection Date'], errors='coerce')
unique_dates = np.unique(df_petr['Collection Date'])
df_petr_2 = pd.DataFrame(np.zeros((0,1)), columns=['Collection Date'])
df_petr_2['Collection Date'] = unique_dates
df_petr_2['Collection Date'] = pd.to_datetime(df_petr_2['Collection Date'], errors='coerce')
for i in range(len(df)):
for j in range(len(df_petr_2)):
if df['Date'][i] == df_petr_2['Collection Date'][j]:
df.loc[i, 'Sticker Received'] = True
break
We can perform logistic regression to classify this data into binary classes, 0: “I did not run for stickers this day”, and 1: “I did run for stickers this day”.
features = ["Steps", "Distance", "Minutes Lightly Active", "Minutes Fairly Active",
"Minutes Very Active", "Activity Calories", "Sticker Received"]
log_model = LogisticRegression(max_iter=10000)
log_model.fit(np.array(df[features[0:6]]), np.array(df[features[6]]));
log_score = log_model.score(np.array(df[features[0:6]]), np.array(df[features[6]]))
print(f"The R^2 value of this Logistic Regression model is: {log_score}.\n")
df_petr = df[features]
df_petr["Sticker Received"] = df_petr["Sticker Received"].astype(int)
scatter_matrix(df_petr, alpha=0.5, figsize=(15, 15), diagonal='kde');
The R^2 value of this Logistic Regression model is: 0.8575851393188855.
/var/folders/fw/7zvj6rks73qb1bvpcbz39q6c0000gn/T/ipykernel_5223/2472311830.py:11: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value instead
See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
df_petr["Sticker Received"] = df_petr["Sticker Received"].astype(int)
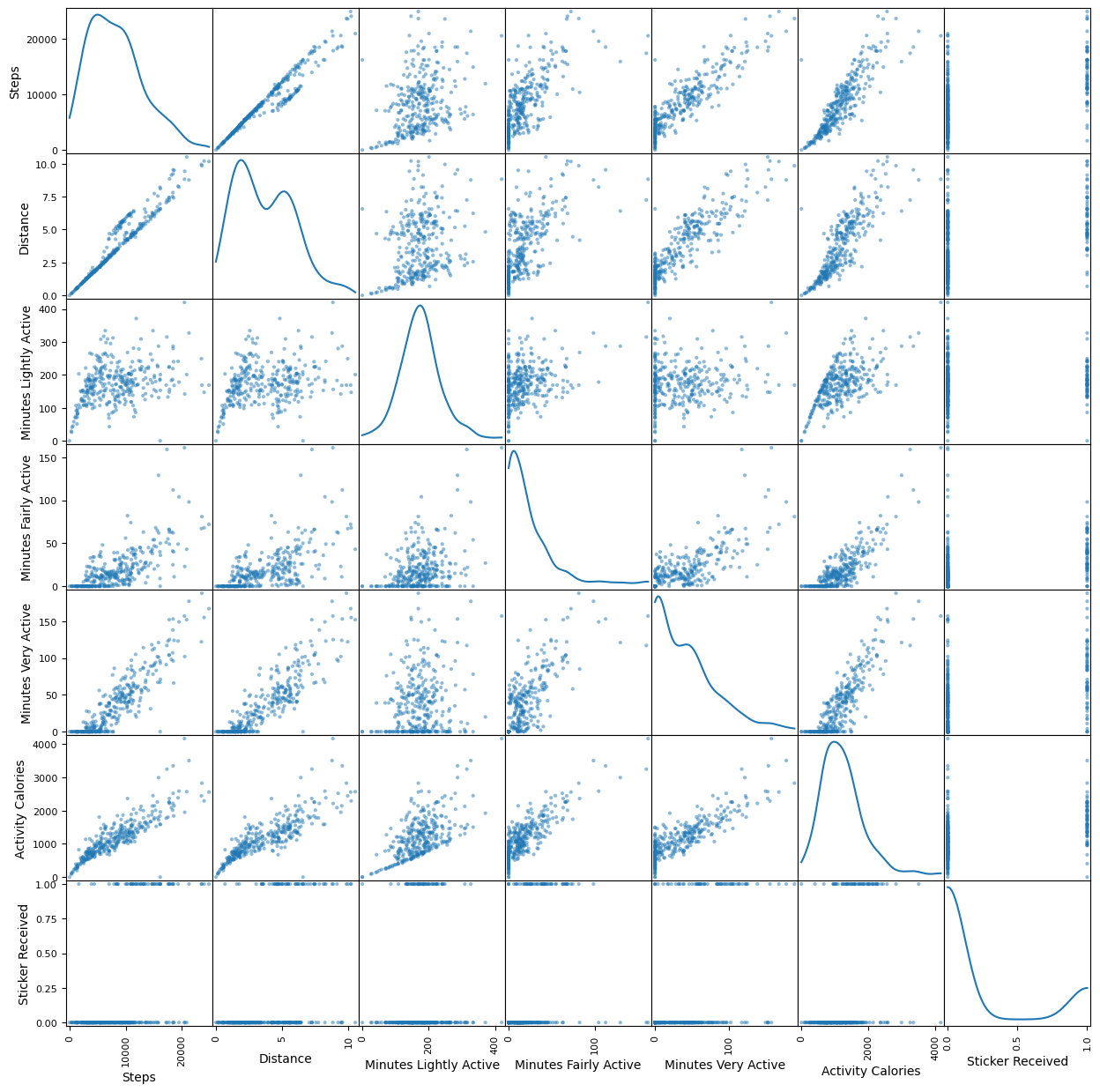
When I was using Linear Regression, it was very easy to tell whether there was a correlation between two different numerical data types, but now that we’re using binary classification, the results are much more nebulous. To remedy this, we can instead plot using logistic regression.
features = ["Steps", "Distance", "Minutes Lightly Active", "Minutes Fairly Active",
"Minutes Very Active", "Activity Calories"]
fig, axes = plt.subplots(3,2,figsize=(20,15))
axes = axes.ravel()
def sigmoid(z):
return 1 / (1 + np.exp(-z))
for i in range(len(features)):
X = np.linspace(df_petr[features[i]].min(), df_petr[features[i]].max(), num=1000)
log_model = LogisticRegression()
log_model.fit(np.array(df_petr[features[i]]).reshape(-1,1), np.array(df_petr["Sticker Received"]))
logistic_prob = sigmoid(log_model.coef_ * X + log_model.intercept_)
axes[i].plot(X.reshape(-1,1), logistic_prob.reshape(-1,1))
axes[i].set_title(f"Logistic Probability of {features[i]}")
axes[i].set_xlabel(f"{features[i]}")
axes[i].set_ylabel("Probability")
axes[i].scatter(np.array(df_petr[features[i]]), np.array(df_petr["Sticker Received"]))
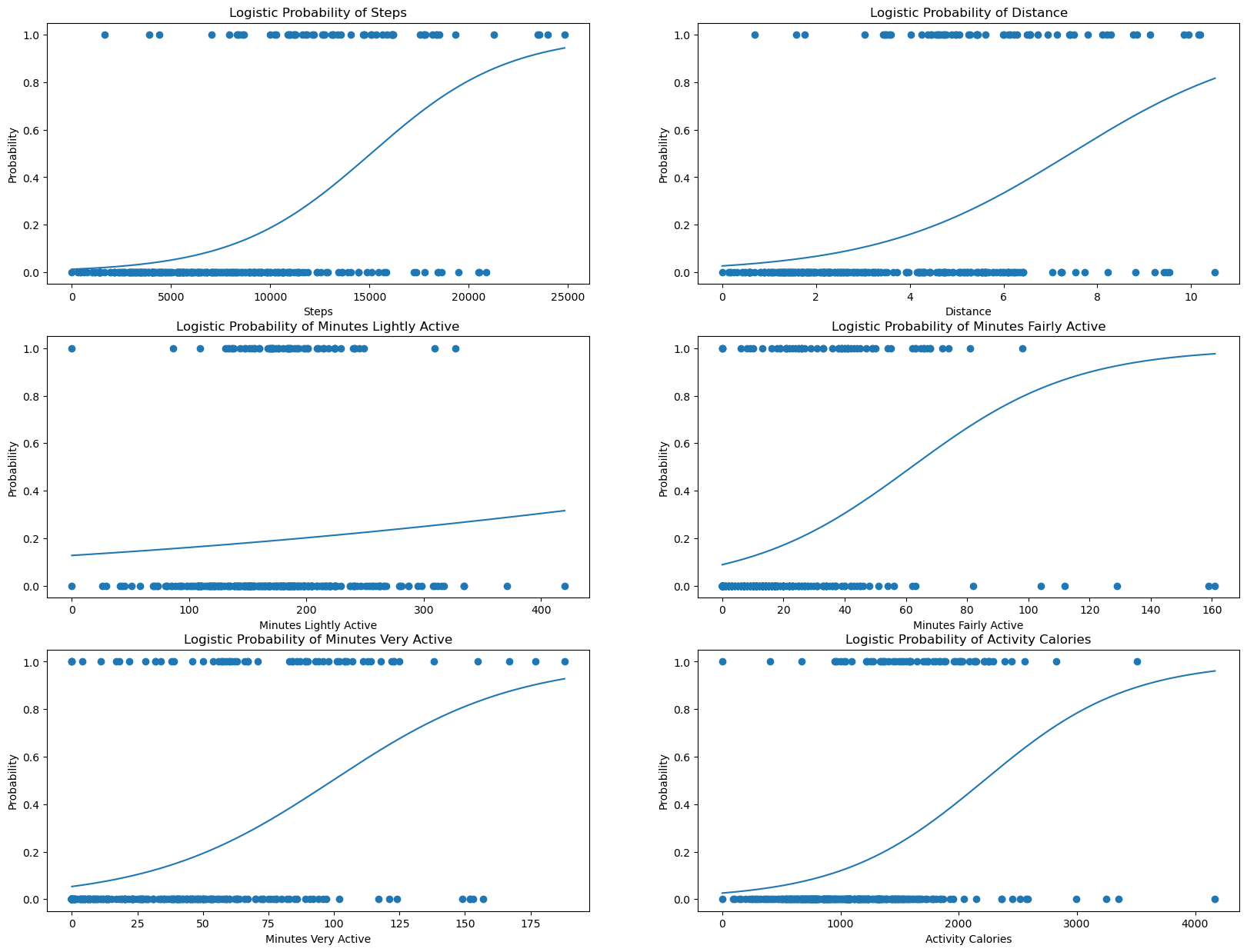
This is much more clear which features correspond to which class: 1, being stickers received, and 0, no sticker received that day. However, as we learned earlier, this model has an R^2 value of roughly 0.85, which is not very clear by breaking it down into individual plots. Clearly, the combination of all of these features make a better model than alone.
To better try and visualize this data, we can use Principal Component Analysis.
from sklearn.decomposition import PCA
features = ["Steps", "Distance", "Minutes Lightly Active", "Minutes Fairly Active",
"Minutes Very Active", "Activity Calories", "Sticker Received"]
fig, ax = plt.subplots(figsize=(8,6))
# We can apply PCA to work on this multi-dimensional model.
pca = PCA(n_components=2)
pca.fit(df_petr)
transformed_data = pca.transform(df_petr)
# Let's visualize the principle components
ax.scatter(transformed_data[:, 0], transformed_data[:, 1], alpha=0.5);
ax.set_xlabel("Principal Component 1")
ax.set_ylabel("Principal Component 2")
ax.set_title("Data After Principal Component Analysis")
Text(0.5, 1.0, 'Data After Principal Component Analysis')
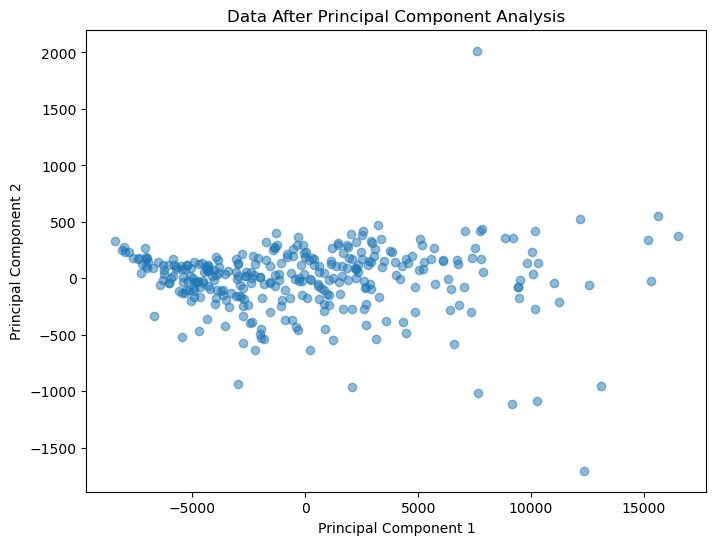
As we can see, our data has been reduced from an incomprehensible 6 dimensions down to just two.
This next section will focus on neural networks, particularly by using the tensorflow library. To be 100% transparent, since I am unfamiliar with the library, I used a few YouTube tutorials to help get started, as well as much of tensorflow’s native documentation. This is one tutorial that I used. However, to prove that I do have some level of understanding of what is being done in the process, I will be annotating what each major step does along the way.
I will be trying to create a model that will be able to accurately predict whether or not the sleep and exercise I received that day is enough to tell if I ran for a sticker that day.
# Reimport tensorflow
import tensorflow as tf
# I am going to be reusing the df library, minus the Date column
df
| Date | Hours Asleep | Minutes Asleep | Minutes Awake | Number of Awakenings | Time in Bed | Minutes REM Sleep | Minutes Light Sleep | Minutes Deep Sleep | Calories Burned | Steps | Distance | Floors | Minutes Sedentary | Minutes Lightly Active | Minutes Fairly Active | Minutes Very Active | Activity Calories | Sticker Received | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2024-05-28 | 5.650000 | 296.0 | 42.0 | 29.0 | 338.0 | 36.0 | 183.0 | 77.0 | 3131.0 | 14451.0 | 5.78 | 37.0 | 684.0 | 185.0 | 40.0 | 89.0 | 1671.0 | False |
| 1 | 2024-05-27 | 7.366667 | 370.0 | 72.0 | 37.0 | 442.0 | 61.0 | 262.0 | 47.0 | 2375.0 | 6989.0 | 4.25 | 0.0 | 1320.0 | 80.0 | 1.0 | 39.0 | 803.0 | False |
| 2 | 2024-05-24 | 8.200000 | 403.0 | 89.0 | 41.0 | 492.0 | 74.0 | 285.0 | 44.0 | 2878.0 | 12209.0 | 4.99 | 28.0 | 977.0 | 171.0 | 19.0 | 62.0 | 1363.0 | True |
| 3 | 2024-05-23 | 3.533333 | 185.0 | 26.0 | 18.0 | 211.0 | 34.0 | 121.0 | 30.0 | 3603.0 | 15120.0 | 5.99 | 23.0 | 812.0 | 198.0 | 54.0 | 113.0 | 2145.0 | True |
| 4 | 2024-05-22 | 4.383333 | 226.0 | 37.0 | 27.0 | 263.0 | 47.0 | 144.0 | 35.0 | 2799.0 | 11740.0 | 4.44 | 22.0 | 867.0 | 188.0 | 37.0 | 23.0 | 1199.0 | False |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 318 | 2023-03-14 | 6.150000 | 322.0 | 46.0 | 37.0 | 368.0 | 87.0 | 184.0 | 51.0 | 2969.0 | 5574.0 | 2.27 | 9.0 | 623.0 | 308.0 | 20.0 | 3.0 | 1463.0 | False |
| 319 | 2023-03-13 | 8.100000 | 426.0 | 60.0 | 53.0 | 486.0 | 118.0 | 227.0 | 81.0 | 2527.0 | 5361.0 | 2.15 | 9.0 | 852.0 | 204.0 | 0.0 | 0.0 | 883.0 | False |
| 320 | 2023-03-12 | 4.750000 | 241.0 | 44.0 | 26.0 | 285.0 | 53.0 | 131.0 | 57.0 | 3004.0 | 6500.0 | 2.79 | 10.0 | 584.0 | 298.0 | 15.0 | 13.0 | 1524.0 | False |
| 321 | 2023-03-11 | 9.833333 | 453.0 | 77.0 | 46.0 | 530.0 | 81.0 | 293.0 | 79.0 | 2720.0 | 5569.0 | 2.28 | 8.0 | 618.0 | 216.0 | 40.0 | 7.0 | 1231.0 | False |
| 322 | 2023-03-10 | 9.333333 | 453.0 | 106.0 | 60.0 | 559.0 | 96.0 | 290.0 | 67.0 | 2972.0 | 6313.0 | 2.59 | 8.0 | 752.0 | 266.0 | 26.0 | 15.0 | 1468.0 | False |
323 rows × 19 columns
# Remove independent variables from the data that we are trying to predict
# That is, X includes everything except date and whether I received a sticker that day.
X = df.drop(['Date', 'Sticker Received'], axis=1)
y = df['Sticker Received'].apply(lambda x: 1 if x==True else 0)
# Create a train test split of data to later test the accuracy of the model.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
View the training data we have collected.
X_train.head()
| Hours Asleep | Minutes Asleep | Minutes Awake | Number of Awakenings | Time in Bed | Minutes REM Sleep | Minutes Light Sleep | Minutes Deep Sleep | Calories Burned | Steps | Distance | Floors | Minutes Sedentary | Minutes Lightly Active | Minutes Fairly Active | Minutes Very Active | Activity Calories | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 235 | 8.650000 | 433.0 | 86.0 | 51.0 | 519.0 | 40.0 | 332.0 | 61.0 | 2706.0 | 10641.0 | 6.09 | 0.0 | 793.0 | 139.0 | 3.0 | 50.0 | 1115.0 |
| 159 | 8.933333 | 455.0 | 80.0 | 50.0 | 535.0 | 115.0 | 260.0 | 80.0 | 3857.0 | 18460.0 | 9.22 | 25.0 | 571.0 | 280.0 | 62.0 | 96.0 | 2520.0 |
| 106 | 7.116667 | 376.0 | 51.0 | 33.0 | 427.0 | 85.0 | 206.0 | 85.0 | 3532.0 | 18152.0 | 9.13 | 23.0 | 835.0 | 183.0 | 63.0 | 98.0 | 2090.0 |
| 274 | 8.383333 | 435.0 | 68.0 | 44.0 | 503.0 | 88.0 | 286.0 | 61.0 | 1750.0 | 395.0 | 0.16 | 1.0 | 1016.0 | 26.0 | 0.0 | 0.0 | 91.0 |
| 57 | 8.900000 | 415.0 | 59.0 | 47.0 | 474.0 | 86.0 | 250.0 | 79.0 | 2927.0 | 8209.0 | 4.26 | 8.0 | 719.0 | 171.0 | 14.0 | 46.0 | 1325.0 |
y_train.head()
235 0
159 0
106 1
274 0
57 0
Name: Sticker Received, dtype: int64
# Sequential will be our primary model class, where each layer has one input and one output.
from tensorflow.keras.models import Sequential
# Dense is a layer without our network, which allows us to create several layers.
from tensorflow.keras.layers import Dense
# Our metric to see how successful our model is
from sklearn.metrics import accuracy_score
I had to learn a bit about sigmoid in relation to ReLU, and it turns out ReLU is used here because it is much easier to compute. For models that decide 0 or 1, simplicity is necessary when there is a requirement of a lot of computing power (and for deep learning models like this one, that is indeed the case). Therefore, for the hidden layers, we use ReLU.
model = Sequential()
# Dense layers with each layer having 32, 64, and 1 nodes, respectively.
# Relu doesn't take raw data out, it takes a minimum of zero and maximum of one, similar to sigmoid.
# Our input data is the same number of dimensions as our dataframe.
model.add(Dense(units=32, activation='relu', input_dim=len(X_train.columns)))
model.add(Dense(units=64, activation='relu'))
# This is what we're trying to predict, so that's why there is only one node.
model.add(Dense(units=1, activation='sigmoid'))
/Users/alexkimm/anaconda3/envs/math9/lib/python3.11/site-packages/keras/src/layers/core/dense.py:87: UserWarning: Do not pass an `input_shape`/`input_dim` argument to a layer. When using Sequential models, prefer using an `Input(shape)` object as the first layer in the model instead.
super().__init__(activity_regularizer=activity_regularizer, **kwargs)
# Compiling our model tells the model what loss we're using, and how it wants to measure success.
model.compile(loss='binary_crossentropy', optimizer='sgd', metrics=['accuracy'])
# BCE is a measure of error, optimizer is an option of how we find that error (and reduce it), and accuracy is clear.
# Iterate our model with 250 times, with 32 points each time.
model.fit(X_train, y_train, epochs=250, batch_size=32)
Epoch 1/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.4787 - loss: 5284039.0000
Epoch 2/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8110 - loss: 0.6841
Epoch 3/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8019 - loss: 0.6746
Epoch 4/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7537 - loss: 0.6698
Epoch 5/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7717 - loss: 0.6617
Epoch 6/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7977 - loss: 0.6503
Epoch 7/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7877 - loss: 0.6458
Epoch 8/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8139 - loss: 0.6347
Epoch 9/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8008 - loss: 0.6315
Epoch 10/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8186 - loss: 0.6201
Epoch 11/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7793 - loss: 0.6254
Epoch 12/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - accuracy: 0.8054 - loss: 0.6117
Epoch 13/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8021 - loss: 0.6081
Epoch 14/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8189 - loss: 0.5964
Epoch 15/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8324 - loss: 0.5854
Epoch 16/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7895 - loss: 0.5978
Epoch 17/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7832 - loss: 0.5958
Epoch 18/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8236 - loss: 0.5736
Epoch 19/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7621 - loss: 0.5982
Epoch 20/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8038 - loss: 0.5747
Epoch 21/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8223 - loss: 0.5610
Epoch 22/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7901 - loss: 0.5748
Epoch 23/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7969 - loss: 0.5686
Epoch 24/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8069 - loss: 0.5606
Epoch 25/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7807 - loss: 0.5721
Epoch 26/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8078 - loss: 0.5540
Epoch 27/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - accuracy: 0.8021 - loss: 0.5542
Epoch 28/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7773 - loss: 0.5669
Epoch 29/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7747 - loss: 0.5662
Epoch 30/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step - accuracy: 0.8095 - loss: 0.5416
Epoch 31/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - accuracy: 0.7896 - loss: 0.5525
Epoch 32/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7772 - loss: 0.5596
Epoch 33/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7725 - loss: 0.5616
Epoch 34/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8131 - loss: 0.5304
Epoch 35/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8146 - loss: 0.5269
Epoch 36/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step - accuracy: 0.7941 - loss: 0.5409
Epoch 37/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7801 - loss: 0.5498
Epoch 38/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7919 - loss: 0.5390
Epoch 39/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8055 - loss: 0.5264
Epoch 40/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7932 - loss: 0.5360
Epoch 41/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8320 - loss: 0.5025
Epoch 42/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8144 - loss: 0.5151
Epoch 43/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8054 - loss: 0.5210
Epoch 44/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7933 - loss: 0.5312
Epoch 45/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - accuracy: 0.7750 - loss: 0.5458
Epoch 46/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - accuracy: 0.8041 - loss: 0.5191
Epoch 47/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7906 - loss: 0.5304
Epoch 48/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7813 - loss: 0.5382
Epoch 49/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8089 - loss: 0.5127
Epoch 50/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8216 - loss: 0.4998
Epoch 51/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8206 - loss: 0.4993
Epoch 52/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7786 - loss: 0.5376
Epoch 53/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8115 - loss: 0.5054
Epoch 54/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8197 - loss: 0.4970
Epoch 55/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8238 - loss: 0.4925
Epoch 56/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7790 - loss: 0.5360
Epoch 57/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step - accuracy: 0.8100 - loss: 0.5056
Epoch 58/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8119 - loss: 0.5027
Epoch 59/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7927 - loss: 0.5208
Epoch 60/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7524 - loss: 0.5608
Epoch 61/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8320 - loss: 0.4801
Epoch 62/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7929 - loss: 0.5194
Epoch 63/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7793 - loss: 0.5330
Epoch 64/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7988 - loss: 0.5125
Epoch 65/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7781 - loss: 0.5334
Epoch 66/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7798 - loss: 0.5312
Epoch 67/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7914 - loss: 0.5192
Epoch 68/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7852 - loss: 0.5252
Epoch 69/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7900 - loss: 0.5196
Epoch 70/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7815 - loss: 0.5284
Epoch 71/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7964 - loss: 0.5118
Epoch 72/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7728 - loss: 0.5372
Epoch 73/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7991 - loss: 0.5079
Epoch 74/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7895 - loss: 0.5185
Epoch 75/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8161 - loss: 0.4884
Epoch 76/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7511 - loss: 0.5612
Epoch 77/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7935 - loss: 0.5133
Epoch 78/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - accuracy: 0.8090 - loss: 0.4954
Epoch 79/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7966 - loss: 0.5091
Epoch 80/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7873 - loss: 0.5195
Epoch 81/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8048 - loss: 0.4991
Epoch 82/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8128 - loss: 0.4893
Epoch 83/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8209 - loss: 0.4794
Epoch 84/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7946 - loss: 0.5102
Epoch 85/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7940 - loss: 0.5107
Epoch 86/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8071 - loss: 0.4948
Epoch 87/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7992 - loss: 0.5040
Epoch 88/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8075 - loss: 0.4938
Epoch 89/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7811 - loss: 0.5257
Epoch 90/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7771 - loss: 0.5306
Epoch 91/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8172 - loss: 0.4814
Epoch 92/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8122 - loss: 0.4873
Epoch 93/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7866 - loss: 0.5188
Epoch 94/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8054 - loss: 0.4953
Epoch 95/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8285 - loss: 0.4663
Epoch 96/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7835 - loss: 0.5226
Epoch 97/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 13ms/step - accuracy: 0.7641 - loss: 0.5470
Epoch 98/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8093 - loss: 0.4898
Epoch 99/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7750 - loss: 0.5333
Epoch 100/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7865 - loss: 0.5186
Epoch 101/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7880 - loss: 0.5167
Epoch 102/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8059 - loss: 0.4938
Epoch 103/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7910 - loss: 0.5128
Epoch 104/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7701 - loss: 0.5397
Epoch 105/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7791 - loss: 0.5281
Epoch 106/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7814 - loss: 0.5252
Epoch 107/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8014 - loss: 0.4994
Epoch 108/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - accuracy: 0.8039 - loss: 0.4961
Epoch 109/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8022 - loss: 0.4983
Epoch 110/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - accuracy: 0.8069 - loss: 0.4922
Epoch 111/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7982 - loss: 0.5034
Epoch 112/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7850 - loss: 0.5205
Epoch 113/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7932 - loss: 0.5097
Epoch 114/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7984 - loss: 0.5029
Epoch 115/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7947 - loss: 0.5079
Epoch 116/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - accuracy: 0.8028 - loss: 0.4972
Epoch 117/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7828 - loss: 0.5234
Epoch 118/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7907 - loss: 0.5130
Epoch 119/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8104 - loss: 0.4871
Epoch 120/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7996 - loss: 0.5014
Epoch 121/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7933 - loss: 0.5097
Epoch 122/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7810 - loss: 0.5258
Epoch 123/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7803 - loss: 0.5266
Epoch 124/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7799 - loss: 0.5272
Epoch 125/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7906 - loss: 0.5133
Epoch 126/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8119 - loss: 0.4851
Epoch 127/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - accuracy: 0.7832 - loss: 0.5230
Epoch 128/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7831 - loss: 0.5231
Epoch 129/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8087 - loss: 0.4891
Epoch 130/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7847 - loss: 0.5211
Epoch 131/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7764 - loss: 0.5320
Epoch 132/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8087 - loss: 0.4891
Epoch 133/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7718 - loss: 0.5382
Epoch 134/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - accuracy: 0.7788 - loss: 0.5288
Epoch 135/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8235 - loss: 0.4699
Epoch 136/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7606 - loss: 0.5528
Epoch 137/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7726 - loss: 0.5371
Epoch 138/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8039 - loss: 0.4956
Epoch 139/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7877 - loss: 0.5171
Epoch 140/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7912 - loss: 0.5124
Epoch 141/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7827 - loss: 0.5236
Epoch 142/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8011 - loss: 0.4994
Epoch 143/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7889 - loss: 0.5155
Epoch 144/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8008 - loss: 0.4999
Epoch 145/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7770 - loss: 0.5311
Epoch 146/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8018 - loss: 0.4984
Epoch 147/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7728 - loss: 0.5366
Epoch 148/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - accuracy: 0.8162 - loss: 0.4794
Epoch 149/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7771 - loss: 0.5311
Epoch 150/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - accuracy: 0.8051 - loss: 0.4939
Epoch 151/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7854 - loss: 0.5201
Epoch 152/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7993 - loss: 0.5016
Epoch 153/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7949 - loss: 0.5074
Epoch 154/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7674 - loss: 0.5441
Epoch 155/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7607 - loss: 0.5530
Epoch 156/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7859 - loss: 0.5195
Epoch 157/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7735 - loss: 0.5358
Epoch 158/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7988 - loss: 0.5023
Epoch 159/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7910 - loss: 0.5126
Epoch 160/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7933 - loss: 0.5096
Epoch 161/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8139 - loss: 0.4821
Epoch 162/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7966 - loss: 0.5052
Epoch 163/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - accuracy: 0.8124 - loss: 0.4842
Epoch 164/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7902 - loss: 0.5137
Epoch 165/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7721 - loss: 0.5379
Epoch 166/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7960 - loss: 0.5060
Epoch 167/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8059 - loss: 0.4927
Epoch 168/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7671 - loss: 0.5443
Epoch 169/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8117 - loss: 0.4854
Epoch 170/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8030 - loss: 0.4970
Epoch 171/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7982 - loss: 0.5032
Epoch 172/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - accuracy: 0.8044 - loss: 0.4951
Epoch 173/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7798 - loss: 0.5274
Epoch 174/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7992 - loss: 0.5018
Epoch 175/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7872 - loss: 0.5177
Epoch 176/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7932 - loss: 0.5099
Epoch 177/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8037 - loss: 0.4960
Epoch 178/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7720 - loss: 0.5377
Epoch 179/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - accuracy: 0.7790 - loss: 0.5285
Epoch 180/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8154 - loss: 0.4805
Epoch 181/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8293 - loss: 0.4622
Epoch 182/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7890 - loss: 0.5153
Epoch 183/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7614 - loss: 0.5516
Epoch 184/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7757 - loss: 0.5329
Epoch 185/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7709 - loss: 0.5393
Epoch 186/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7860 - loss: 0.5193
Epoch 187/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7839 - loss: 0.5222
Epoch 188/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8081 - loss: 0.4898
Epoch 189/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7732 - loss: 0.5364
Epoch 190/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 6ms/step - accuracy: 0.7767 - loss: 0.5319
Epoch 191/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8190 - loss: 0.4750
Epoch 192/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7877 - loss: 0.5171
Epoch 193/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7942 - loss: 0.5084
Epoch 194/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7971 - loss: 0.5044
Epoch 195/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7719 - loss: 0.5385
Epoch 196/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8130 - loss: 0.4829
Epoch 197/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7851 - loss: 0.5206
Epoch 198/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7808 - loss: 0.5263
Epoch 199/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7977 - loss: 0.5037
Epoch 200/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7900 - loss: 0.5140
Epoch 201/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7687 - loss: 0.5423
Epoch 202/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7908 - loss: 0.5129
Epoch 203/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7801 - loss: 0.5273
Epoch 204/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8069 - loss: 0.4914
Epoch 205/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8109 - loss: 0.4859
Epoch 206/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8189 - loss: 0.4752
Epoch 207/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8039 - loss: 0.4953
Epoch 208/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7912 - loss: 0.5124
Epoch 209/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8047 - loss: 0.4942
Epoch 210/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7969 - loss: 0.5047
Epoch 211/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8056 - loss: 0.4929
Epoch 212/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8046 - loss: 0.4943
Epoch 213/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7863 - loss: 0.5191
Epoch 214/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7878 - loss: 0.5170
Epoch 215/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7927 - loss: 0.5104
Epoch 216/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8086 - loss: 0.4889
Epoch 217/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8062 - loss: 0.4921
Epoch 218/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7776 - loss: 0.5309
Epoch 219/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7692 - loss: 0.5421
Epoch 220/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7865 - loss: 0.5187
Epoch 221/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7977 - loss: 0.5036
Epoch 222/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7922 - loss: 0.5110
Epoch 223/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8077 - loss: 0.4900
Epoch 224/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7897 - loss: 0.5144
Epoch 225/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7785 - loss: 0.5296
Epoch 226/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8035 - loss: 0.4957
Epoch 227/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7697 - loss: 0.5413
Epoch 228/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - accuracy: 0.7966 - loss: 0.5052
Epoch 229/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.7984 - loss: 0.5027
Epoch 230/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7993 - loss: 0.5014
Epoch 231/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8017 - loss: 0.4982
Epoch 232/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8191 - loss: 0.4751
Epoch 233/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7894 - loss: 0.5147
Epoch 234/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8131 - loss: 0.4830
Epoch 235/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7796 - loss: 0.5280
Epoch 236/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8031 - loss: 0.4963
Epoch 237/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7840 - loss: 0.5221
Epoch 238/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8262 - loss: 0.4650
Epoch 239/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7799 - loss: 0.5278
Epoch 240/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8023 - loss: 0.4973
Epoch 241/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7991 - loss: 0.5017
Epoch 242/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - accuracy: 0.8161 - loss: 0.4784
Epoch 243/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7816 - loss: 0.5256
Epoch 244/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.8290 - loss: 0.4605
Epoch 245/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7707 - loss: 0.5407
Epoch 246/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7893 - loss: 0.5151
Epoch 247/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8056 - loss: 0.4927
Epoch 248/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8193 - loss: 0.4740
Epoch 249/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.8119 - loss: 0.4841
Epoch 250/250
9/9 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - accuracy: 0.7814 - loss: 0.5259
<keras.src.callbacks.history.History at 0x13f12dc50>
y_predicted = model.predict(X_test)
y_predicted = [0 if val < 0.5 else 1 for val in y_predicted]
3/3 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
I will say that I ran this y_predicted many times and each time it cmae out as an array of just zeros, which suggests that the model ends up thinking that a sticker is not collected on most days, which makes sense. This may be due to the fact that the number of days where stickers were collected is around 90 and the total number of days in this entire dataset is more than 300, meaning it is vanishingly unlikely that I collected a sticker that day. Even so, this uniform guess of zeros might be something I look into in the future.
np.array(y_predicted)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
accuracy_score(y_test, y_predicted)
0.8615384615384616
Thus, this model turns out to be relatively accurate, being able to correctly guess if I ran for stickers 86% of the time.
Thus, we have come to a conclusion with several interesting discoveries. Firstly, at least for my own sleep, there does not seem to be a significant correlation between the amount of sleep and exercise that I receive. In the heatmap that we looked at above, there was at best a very weak positive correlation.
Then, we looked at my sleep and exercise individually. When it comes to sleep, the best way to predict how many times I am awaken at night, the best determiner out of how many minutes restless, REM, Light, and Deep sleep, turns out to be a combination of all of these different features, with a model that had a R^2 score of about 0.76.
For exercise, I performed logistic regression to predict a new variable that I put into binary classes, whether I ran for a sticker that day or not. It turns out, the model had an R^2 value of about 0.85, meaning the model fit quite well.
Finally, we performed a neural network with two layers with all of the variables (minus the date) to test if these variables could altogether predict whether I ran for a sticker that day. The network was very good, receiving similar results to the R^2 score of the logistic model, with an accuracy of 86%.
For future projects, I think it might be better to run the neural network with more layers or greater epochs. I used 2 layers and 250 generations because my computer began to run more slowly if I increased any of these values.
Thank you for reading this project.