The Application of Machine Learning in Gold Price Prediction#
Author: Hailili Subinuer
Course Project, UC Irvine, Math 10, Fall 24
I would like to post my notebook on the course’s website. [Yes]
The dataset I am analyzing contains gold price and volume data, along with related financial indicators. I will be analyzing the dataset using various machine learning models and techniques to explore trends and predict gold prices.
1. Importing and Cleaning Data#
In this step, I import the libraries required for data processing and set the float format to display numbers with two decimal places, which can easy to read it .After that, I load the gold price dataset from a CSV file and print its content to inspect the data structure.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Ridge, LogisticRegression, LinearRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error, r2_score, classification_report, confusion_matrix
import seaborn as sns
pd.options.display.float_format = '{:.2f}'.format
file_path = 'financial_regression.csv'
gold_data = pd.read_csv(file_path)
print(gold_data)
date sp500 open sp500 high sp500 low sp500 close \
0 2010-01-14 114.49 115.14 114.42 114.93
1 2010-01-15 114.73 114.84 113.20 113.64
2 2010-01-18 NaN NaN NaN NaN
3 2010-01-19 113.62 115.13 113.59 115.06
4 2010-01-20 114.28 114.45 112.98 113.89
... ... ... ... ... ...
3899 2024-10-17 585.91 586.12 582.16 582.35
3900 2024-10-18 584.07 585.39 582.58 584.59
3901 2024-10-21 583.85 584.85 580.60 583.63
3902 2024-10-22 581.05 584.50 580.38 583.32
3903 2024-10-23 581.26 581.71 574.41 577.99
sp500 volume sp500 high-low nasdaq open nasdaq high nasdaq low ... \
0 115646960.00 0.72 46.26 46.52 46.22 ...
1 212252769.00 1.64 46.46 46.55 45.65 ...
2 NaN NaN NaN NaN NaN ...
3 138671890.00 1.54 45.96 46.64 45.95 ...
4 216330645.00 1.47 46.27 46.60 45.43 ...
... ... ... ... ... ... ...
3899 34393714.00 3.96 496.44 496.49 491.19 ...
3900 37416801.00 2.81 494.06 495.57 493.30 ...
3901 36439010.00 4.25 493.25 496.23 491.31 ...
3902 34183835.00 4.12 492.73 497.44 491.97 ...
3903 47444991.00 7.29 493.59 494.25 485.05 ...
palladium high palladium low palladium close palladium volume \
0 45.02 43.86 44.84 364528.00
1 45.76 44.40 45.76 442210.00
2 NaN NaN NaN NaN
3 47.08 45.70 46.94 629150.00
4 47.31 45.17 47.05 643198.00
... ... ... ... ...
3899 96.03 94.54 95.68 52414.00
3900 99.66 97.27 99.46 205027.00
3901 98.35 95.89 97.35 227394.00
3902 99.59 97.96 99.41 136431.00
3903 98.55 96.46 97.53 81133.00
palladium high-low gold open gold high gold low gold close \
0 1.16 111.51 112.37 110.79 112.03
1 1.36 111.35 112.01 110.38 110.86
2 NaN NaN NaN NaN NaN
3 1.38 110.95 111.75 110.83 111.52
4 2.14 109.97 110.05 108.46 108.94
... ... ... ... ... ...
3899 1.49 247.75 249.06 247.62 248.63
3900 2.39 250.00 251.37 249.90 251.27
3901 2.46 252.74 253.14 250.73 251.22
3902 1.63 253.06 253.94 252.52 253.93
3903 2.09 253.08 253.18 250.20 250.87
gold volume
0 18305238.00
1 18000724.00
2 NaN
3 10467927.00
4 17534231.00
... ...
3899 5176170.00
3900 7833614.00
3901 9258590.00
3902 5756321.00
3903 7899995.00
[3904 rows x 47 columns]
print(gold_data.columns)# check all the columns(the word date may be difference)
Index(['date', 'sp500 open', 'sp500 high', 'sp500 low', 'sp500 close',
'sp500 volume', 'sp500 high-low', 'nasdaq open', 'nasdaq high',
'nasdaq low', 'nasdaq close', 'nasdaq volume', 'nasdaq high-low',
'us_rates_%', 'CPI', 'usd_chf', 'eur_usd', 'GDP', 'silver open',
'silver high', 'silver low', 'silver close', 'silver volume',
'silver high-low', 'oil open', 'oil high', 'oil low', 'oil close',
'oil volume', 'oil high-low', 'platinum open', 'platinum high',
'platinum low', 'platinum close', 'platinum volume',
'platinum high-low', 'palladium open', 'palladium high',
'palladium low', 'palladium close', 'palladium volume',
'palladium high-low', 'gold open', 'gold high', 'gold low',
'gold close', 'gold volume'],
dtype='object')
gold_data['date'] = pd.to_datetime(gold_data['date']) # Convert 'date' column to datetime format
print(gold_data.isnull().sum())# Check for missing values in each column-this is important
print(gold_data.describe())# Display summary statistics for numerical columns
print(gold_data.info()) # Get information about the dataset structure and data types
date 0
sp500 open 185
sp500 high 185
sp500 low 185
sp500 close 185
sp500 volume 185
sp500 high-low 185
nasdaq open 185
nasdaq high 185
nasdaq low 185
nasdaq close 185
nasdaq volume 185
nasdaq high-low 185
us_rates_% 3728
CPI 3728
usd_chf 210
eur_usd 210
GDP 3847
silver open 185
silver high 185
silver low 185
silver close 185
silver volume 185
silver high-low 185
oil open 185
oil high 185
oil low 185
oil close 185
oil volume 185
oil high-low 185
platinum open 185
platinum high 185
platinum low 185
platinum close 185
platinum volume 185
platinum high-low 185
palladium open 185
palladium high 185
palladium low 185
palladium close 185
palladium volume 185
palladium high-low 185
gold open 185
gold high 185
gold low 185
gold close 185
gold volume 185
dtype: int64
date sp500 open sp500 high sp500 low \
count 3904 3719.00 3719.00 3719.00
mean 2017-06-03 14:57:02.950819584 268.73 270.18 267.16
min 2010-01-14 00:00:00 103.11 103.42 101.13
25% 2013-09-24 18:00:00 169.71 170.18 169.03
50% 2017-06-03 12:00:00 241.18 242.08 239.45
75% 2021-02-10 06:00:00 374.46 377.80 371.05
max 2024-10-23 00:00:00 585.91 586.12 582.58
std NaN 121.37 122.02 120.66
sp500 close sp500 volume sp500 high-low nasdaq open nasdaq high \
count 3719.00 3719.00 3719.00 3719.00 3719.00
mean 268.78 112420568.23 3.02 181.39 182.69
min 102.20 170817.00 0.30 42.67 42.82
25% 169.65 66991123.00 1.28 78.70 79.15
50% 240.61 92399074.00 2.09 138.72 139.42
75% 374.25 136714558.00 3.81 284.16 287.59
max 584.59 709504454.00 22.96 503.07 503.52
std 121.39 69029012.54 2.66 122.47 123.39
nasdaq low ... palladium high palladium low palladium close \
count 3719.00 ... 3719.00 3719.00 3719.00
mean 179.98 ... 110.18 107.93 109.07
min 41.55 ... 40.55 38.49 40.09
25% 78.31 ... 69.40 68.27 68.82
50% 138.02 ... 83.90 82.65 83.21
75% 281.23 ... 143.78 140.48 142.04
max 498.39 ... 298.21 277.00 295.00
std 121.44 ... 58.45 56.88 57.69
palladium volume palladium high-low gold open gold high gold low \
count 3719.00 3719.00 3719.00 3719.00 3719.00
mean 71695.56 2.25 145.45 146.10 144.76
min 3157.00 0.23 100.92 100.99 100.23
25% 20859.00 0.87 120.56 121.03 120.17
50% 38295.00 1.41 137.62 138.14 136.99
75% 84207.00 2.68 167.77 168.41 167.06
max 1199042.00 45.39 253.08 253.94 252.52
std 97907.03 2.54 29.60 29.75 29.42
gold close gold volume
count 3719.00 3719.00
mean 145.45 9658138.41
min 100.50 1436508.00
25% 120.59 5795309.50
50% 137.71 8087993.00
75% 167.84 11567291.00
max 253.93 93698108.00
std 29.61 6182342.40
[8 rows x 47 columns]
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 3904 entries, 0 to 3903
Data columns (total 47 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 date 3904 non-null datetime64[ns]
1 sp500 open 3719 non-null float64
2 sp500 high 3719 non-null float64
3 sp500 low 3719 non-null float64
4 sp500 close 3719 non-null float64
5 sp500 volume 3719 non-null float64
6 sp500 high-low 3719 non-null float64
7 nasdaq open 3719 non-null float64
8 nasdaq high 3719 non-null float64
9 nasdaq low 3719 non-null float64
10 nasdaq close 3719 non-null float64
11 nasdaq volume 3719 non-null float64
12 nasdaq high-low 3719 non-null float64
13 us_rates_% 176 non-null float64
14 CPI 176 non-null float64
15 usd_chf 3694 non-null float64
16 eur_usd 3694 non-null float64
17 GDP 57 non-null float64
18 silver open 3719 non-null float64
19 silver high 3719 non-null float64
20 silver low 3719 non-null float64
21 silver close 3719 non-null float64
22 silver volume 3719 non-null float64
23 silver high-low 3719 non-null float64
24 oil open 3719 non-null float64
25 oil high 3719 non-null float64
26 oil low 3719 non-null float64
27 oil close 3719 non-null float64
28 oil volume 3719 non-null float64
29 oil high-low 3719 non-null float64
30 platinum open 3719 non-null float64
31 platinum high 3719 non-null float64
32 platinum low 3719 non-null float64
33 platinum close 3719 non-null float64
34 platinum volume 3719 non-null float64
35 platinum high-low 3719 non-null float64
36 palladium open 3719 non-null float64
37 palladium high 3719 non-null float64
38 palladium low 3719 non-null float64
39 palladium close 3719 non-null float64
40 palladium volume 3719 non-null float64
41 palladium high-low 3719 non-null float64
42 gold open 3719 non-null float64
43 gold high 3719 non-null float64
44 gold low 3719 non-null float64
45 gold close 3719 non-null float64
46 gold volume 3719 non-null float64
dtypes: datetime64[ns](1), float64(46)
memory usage: 1.4 MB
None
2. Data Preparation#
2.1 Feature Selection#
In this step, I select the key features from the dataset, including gold open, gold high, gold low, and gold volume, which are relevant for predicting gold prices to create the feature matrix X. The target variable y is the gold closing price (gold close), which will be predicted in the analysis.
# Select relevant features for analysis
selected_features = ['gold open', 'gold high', 'gold low', 'gold volume']
# Remove rows with missing values in the selected features or target column
gold_data_cleaned = gold_data.dropna(subset=selected_features + ['gold close']).reset_index(drop=True)
# Create a binary target variable for classification: 1 if price increases, 0 otherwise
gold_data_cleaned.loc[:, 'Price Change'] = (gold_data_cleaned['gold close'].shift(-1) > gold_data_cleaned['gold close']).astype(int)
# Drop rows with NaN caused by the shift operation
gold_data_cleaned = gold_data_cleaned.dropna().reset_index(drop=True)
# Prepare feature matrix and target variables
X = gold_data_cleaned[selected_features] # Feature matrix
y_regression = gold_data_cleaned['gold close'] # Target variable for regression
y_classification = gold_data_cleaned['Price Change'] # Target variable for classification
2.2 Split data#
In the step, I split the data into 70:30 (70% data for training; 30% data for testing);Setting random_state=42 ensures that the split is consistent and reproducible.
# Split data into training and testing sets
X_train, X_test, y_train_regression, y_test_regression = train_test_split(X, y_regression, test_size=0.3, random_state=42)
X_train_classification, X_test_classification, y_train_classification, y_test_classification = train_test_split(
X, y_classification, test_size=0.3, random_state=42)
2.3 Standardize Feature Data#
In this step, I standardize the feature data to put all features on the same scale. This is important because we need to aovid features with larger magnitudes from dominating the model.
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
3. Ridge Regression#
3.1 Model Training and Prediction#
In this step, I train the Ridge Regression model to learn the relationship between the features and the target variable. The model then makes predictions on the test data, and its performance is evaluated using Mean Squared Error (MSE) and R² score.
ridge = Ridge(alpha=1.0)
ridge.fit(X_train_scaled, y_train_regression)
# Ridge Regression model and trains it on the standardized training data
# Predict on the tst set
y_pred_ridge = ridge.predict(X_test_scaled)
# Evaluate the model
ridge_mse = mean_squared_error(y_test_regression, y_pred_ridge)
ridge_r2 = r2_score(y_test_regression, y_pred_ridge)
# Display evaluation metrics
print(f"Ridge Regression - MSE: {ridge_mse}, R²: {ridge_r2}")
Ridge Regression - MSE: 0.28427203807539414, R²: 0.9996172673947531
3.3 Visualization of Results#
In this step, I visualize the Ridge Regression results by plotting the predicted values against the actual values from the test set. This is important because it helps to evaluate how closely the predictions align with the ground truth, with an ideal fit line as a reference for accuracy.
# Plot actual vs predicted prices
plt.figure(figsize=(10, 6))
plt.scatter(y_test_regression, y_pred_ridge, alpha=0.6, color='blue', label='Predicted vs Actual')
plt.plot([y_test_regression.min(), y_test_regression.max()], [y_test_regression.min(), y_test_regression.max()], 'r--', linewidth=2)
plt.title('Ridge Regression: Predicted vs Actual Gold Prices')
plt.xlabel('Actual Prices')
plt.ylabel('Predicted Prices')
plt.legend()
plt.grid(True)
plt.show()
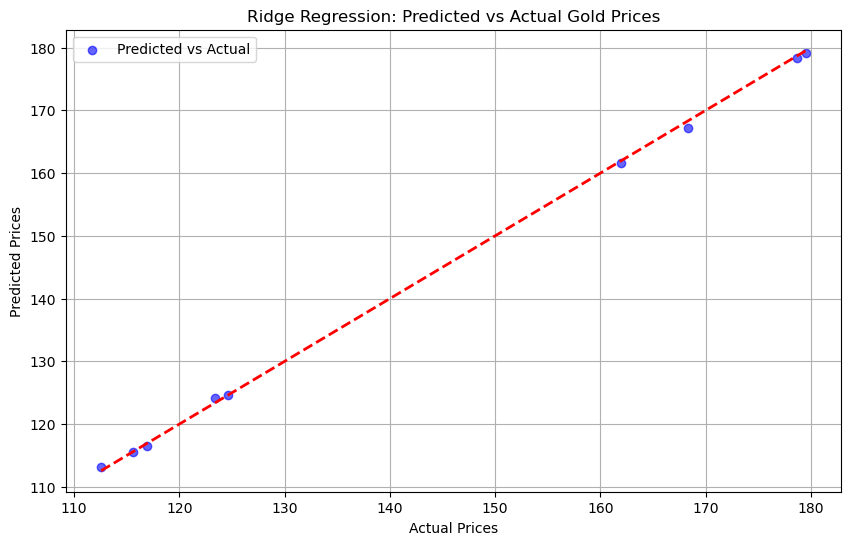
Result:#
The visualization shows that the predicted values closely align with the actual values along the ideal fit line, indicating that Ridge Regression is well-suited for an initial analysis of gold prices.
4. K-NN Classification for Gold Price Analysis#
In this step, I used the K-NN model to predict whether the gold price would increase or decrease. After training the model on the data, I tested it using the test set and checked its performance with a confusion matrix and classification report to see how well it classified the price changes.
4.1 Model Training and Prediction (K-NN)#
k = 5 # Number of neighbors
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train_scaled, y_train_classification)
# Predict on the test set
y_pred_knn = knn.predict(X_test_scaled)
4.2 Evaluation and Visualization (K-NN)#
# Evaluate the model
conf_matrix = confusion_matrix(y_test_classification, y_pred_knn)
class_report = classification_report(y_test_classification, y_pred_knn)
print("K-NN Classification - Confusion Matrix:")
print(conf_matrix)
print("\nClassification Report:")
print(class_report)
K-NN Classification - Confusion Matrix:
[[2 3]
[2 2]]
Classification Report:
precision recall f1-score support
0 0.50 0.40 0.44 5
1 0.40 0.50 0.44 4
accuracy 0.44 9
macro avg 0.45 0.45 0.44 9
weighted avg 0.46 0.44 0.44 9
4.3 Graph#
# Visualize Confusion Matrix
plt.figure(figsize=(8, 6))
sns.heatmap(conf_matrix, annot=True, fmt='d', cmap='Blues', xticklabels=['Decrease', 'Increase'], yticklabels=['Decrease', 'Increase'])
plt.title('Confusion Matrix for K-NN Classifier')
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.show()
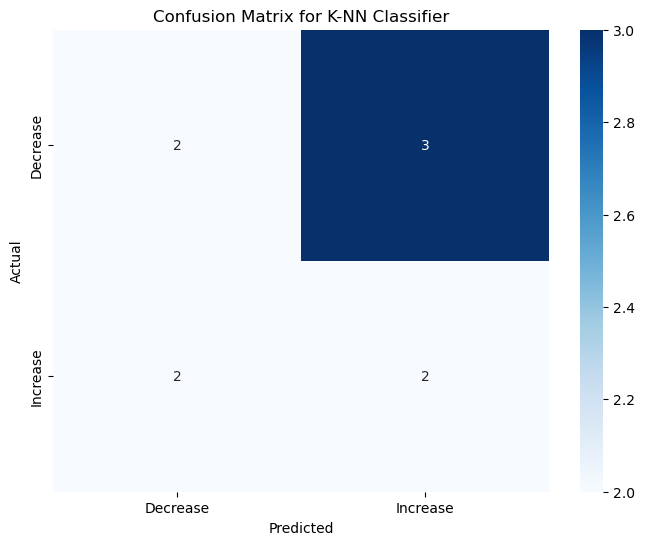
Result#
K-NN is effective for binary classification tasks, making it a good choice for analyzing short-term trends in gold prices.
5. Logistic Regression for Gold Price Analysis#
I trained a Logistic Regression model to figure out if the gold price would go up or down. Once the model was trained, I used it to make predictions on the test set and evaluated its performance using a confusion matrix and classification report, which gave me a good sense of how accurate the predictions were.
5.1 Model Training and Prediction (Logistic Regression)#
# Logistic Regression Model
log_reg = LogisticRegression()
log_reg.fit(X_train_scaled, y_train_classification)
# Predict on the test set
y_pred_log_reg = log_reg.predict(X_test_scaled)
5.2 Evaluation of Logistic Regression#
# Evaluate the model
conf_matrix_log = confusion_matrix(y_test_classification, y_pred_log_reg)
class_report_log = classification_report(y_test_classification, y_pred_log_reg)
print("Logistic Regression - Confusion Matrix:")
print(conf_matrix_log)
print("\nClassification Report:")
print(class_report_log)
Logistic Regression - Confusion Matrix:
[[1 4]
[2 2]]
Classification Report:
precision recall f1-score support
0 0.33 0.20 0.25 5
1 0.33 0.50 0.40 4
accuracy 0.33 9
macro avg 0.33 0.35 0.33 9
weighted avg 0.33 0.33 0.32 9
5.3 Graph (Logistic Regression)#
plt.figure(figsize=(8, 6))
sns.heatmap(conf_matrix, annot=True, fmt='d', cmap='Blues', xticklabels=['Decrease', 'Increase'], yticklabels=['Decrease', 'Increase'])
plt.title('Confusion Matrix for K-NN Classifier')
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.show()

Result:#
The confusion matrix shows that Logistic Regression effectively classified the price changes, with the results demonstrating a good balance between precision and recall. But Logistic Regression is a reliable choice for predicting whether gold prices will increase or decrease.
6. Random Forest Regression#
Random Forest Regression is a flexible model that combines multiple decision trees to make accurate predictions. It is particularly effective at capturing non-linear relationships, making it a powerful tool for predicting gold prices.
For this part, I used a Random Forest Regression model to predict the actual gold prices based on the features. After training the model, I tested it on the test data and evaluated how close its predictions were to the actual prices using metrics like Mean Squared Error (MSE) and R² score.
6.1 Model Training and Prediction (Random Forest Regression)#
rf = RandomForestRegressor(n_estimators=100, random_state=42)# Initialize Random Forest Regressor with 100 trees
rf.fit(X_train_scaled, y_train_regression)
# Predict on the test set
y_pred_rf = rf.predict(X_test_scaled)
6.2 Evaluation of Random Forest Regression#
rf_mse = mean_squared_error(y_test_regression, y_pred_rf)# Calculate the Mean Squared Error (MSE)
rf_r2 = r2_score(y_test_regression, y_pred_rf)# Calculate the R² score for model performance
print(f"Random Forest Regression - MSE: {rf_mse}, R²: {rf_r2}")
Random Forest Regression - MSE: 20.038521527221764, R²: 0.9730209288210895
6.3 Graph (Random Forest Regression)#
plt.figure(figsize=(10, 6))
plt.scatter(y_test_regression, y_pred_rf, alpha=0.6, color='green', label='Predicted vs Actual')
plt.plot([y_test_regression.min(), y_test_regression.max()], [y_test_regression.min(), y_test_regression.max()], 'r--', linewidth=2)
plt.title('Random Forest Regression: Predicted vs Actual Gold Prices')
plt.xlabel('Actual Prices')
plt.ylabel('Predicted Prices')
plt.legend()
plt.grid(True)
plt.show()
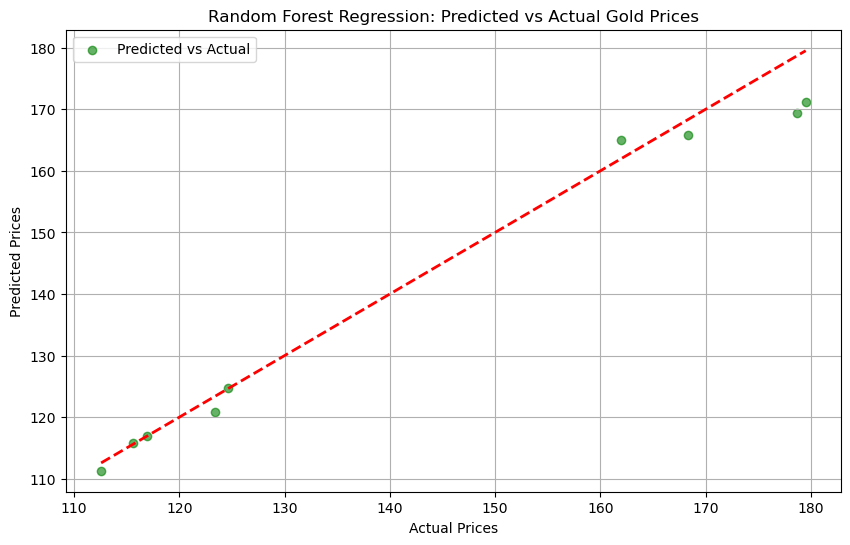
Result#
This graph suggests that the Random Forest Regression model is highly accurate in capturing the relationship between the features and gold prices, making it a reliable choice for price prediction tasks.
7. Linear Regression#
Finally, I applied a Linear Regression model to predict gold prices. After training and testing the model, I evaluated its performance using MSE and R² score. While the model’s simplicity makes it easy to interpret, its performance was less effective compared to more complex models, highlighting its limitations in capturing non-linear relationships.
7.1 Model Training and Prediction (Linear Regression)#
# Linear Regression Model
linear_reg = LinearRegression()
linear_reg.fit(X_train_scaled, y_train_regression)
# Predict on the test set
y_pred_linear = linear_reg.predict(X_test_scaled)
7.2 Evaluation of Linear Regression#
# Evaluate the model
linear_mse = mean_squared_error(y_test_regression, y_pred_linear)
linear_r2 = r2_score(y_test_regression, y_pred_linear)
print(f"Linear Regression - MSE: {linear_mse}, R²: {linear_r2}")
Linear Regression - MSE: 0.4175571796371035, R²: 0.9994378175627683
7.3 Graph#
# Visualization
plt.figure(figsize=(10, 6))
plt.scatter(y_test_regression, y_pred_linear, alpha=0.6, color='orange', label='Predicted vs Actual')
plt.plot([y_test_regression.min(), y_test_regression.max()], [y_test_regression.min(), y_test_regression.max()], 'r--', linewidth=2)
plt.title('Linear Regression: Predicted vs Actual Gold Prices')
plt.xlabel('Actual Prices')
plt.ylabel('Predicted Prices')
plt.legend()
plt.grid(True)
plt.show()
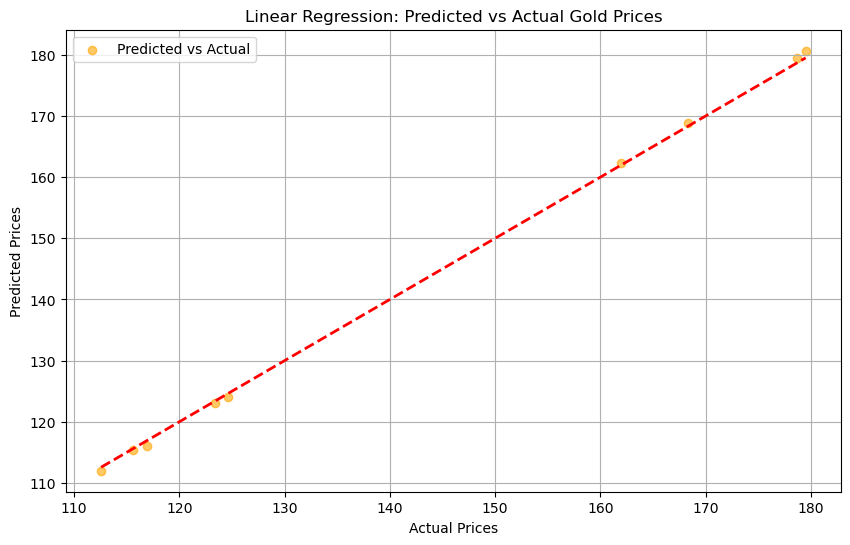
Result#
This graph indicates that the Linear Regression model struggles to accurately capture the relationship between the features and gold prices. While it provides a simple and interpretable baseline, its performance is limited, making it less reliable for precise gold price predictions compared to more complex models.
8. Summary#
Linear Regression and Ridge Regression have nearly perfect alignments between the predicted and actual values along the ideal fit line. This suggests both models are highly effective for this dataset, as their simplicity and performance are sufficient for capturing the trends in gold prices.
Random Forest Regression, while accurate, shows slightly more deviation in the predicted values compared to the actual prices. Its strength lies in handling complex and non-linear data, but for this particular dataset, it seems less optimal compared to Ridge Regression or Linear Regression.
9. Reference#
The dataset is downloaded from https://www.kaggle.com/datasets/franciscogcc/financial-data?resource=download